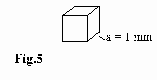
4.3 Quantitative determination of the structure
4.3.1 Determination of the mean distance between two particles
For the quantitative determination of the structure first the condition in open space is contemplated, corresponding to figure 1. The mean distance between two adjacent particles is essential because it is required for the connection to l and hence to the known characteristics of electromagnetic waves.
The open space is interspersed with electromagnetic waves, so is a hollow space.
A hollow space can be considered as a black body. Its spectrum of radiation is only a function of temperature. Such a radiation hits earth as 3 K-radiation from all directions of space. This is a special radiation, giving no direction any preference. It is therefore of a fundamental nature. It is near at hand to derive the wanted mean distance between two adjacent particles from this radiation.
It is known according to /1/: at 3 K: 103 photons / cm3 or 1photon / mm3.
Consequently, the space for a photon is a cube with the side length of a =1 mm (Fig.5):
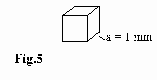
That is the space for a photon or, according to the description above, for one l, but it does not say anything about the distance between two adjacent particles.
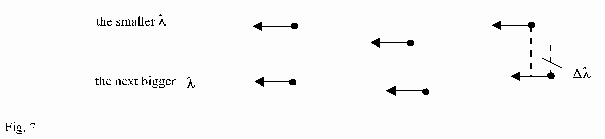
Imagine all l arranged according to size in a certain volume as follows in Fig.6.
Each l is simplified represented by an arrow.
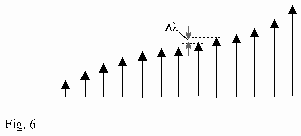
Because there are a finite number of l, this arrangement is possible. In a definite area there are a lot of nearly identical l. This is the area around lmax in the distribution-curve of the electromagnetic radiation. The area of smaller and larger l can be possibly considered as a statistical deviation.
If you ask, how much l will increase by the length Dl when changing from l to the next bigger l in the area lmax, than you get as answer as well the mean distance between two adjacent particles (Fig.7).
Presented:
The problem of the distance between two particles appeared during the search of the mechanism of the redshift of light.
The distance of light-particles between two 3-particle-collisions was needed. For that the determination of the distance between two adjacent particles in the 3 K-space is the basis.
The number of photons (connected with a definite volumen) in the interval of frequence dn is shown, valid for a defined temperature and radiation of a black body:
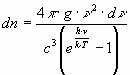
As the distance is here of interest, l instead of n is used:
![]()
dn =
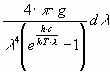
To get the distance between two adjacent particles in the 3 K-space we have to answer the following question: "How long must be dl to increase dn by one photon and to find the next particle?"
In illustration of this question look at figure 8 and 9.
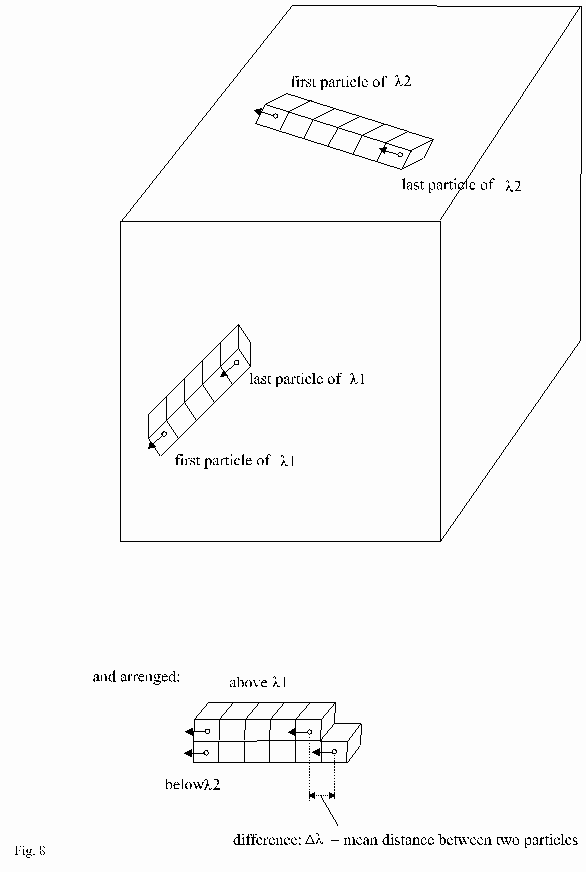
simplified presentation in figure 9:
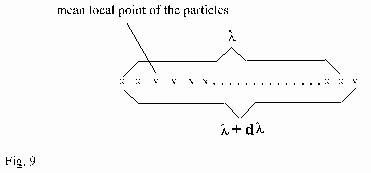
if Dn=1 and
![]()
then follows:
![]()
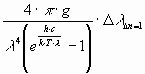
The value of g is to be set at 2 for an electromagnetical wave, consisting of two components. The values of T and l are to be set for the quantitative evaluation as follows:
For the value of T the result of measurement by satellite COBE will be used:
T=(2.726+ 0.004)°K.
For l each possible wave-length can be chosen. One may use the most frequent wave-length and consider the other wave-length as statistical deviations.
The most frequent wave-length is lmax =1.05mm, also known as a result of the measurement by satellite COBE.
Hence, the wanted mean distance between two adjacent particles is as follows:
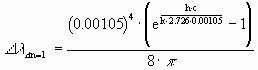
![]()
This value will be of fundamental significance in the calculation of the
examples.
Considering the deflection of light close to the sun, another imaginary formation of particles in a determined volume ( for example 1m3) was suitable:
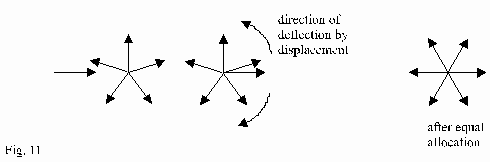
All particles originate in one point but they move in different directions. These particles are represented by arrows by Fig.10:
With that the number of directions being simultaneously in this volume is fixed. The directions are probably equal distributed in space which is only a little disturbed by structures such as light or mass. If a photon arrives at this volume, it is to be integrated in the beam of rays.
The striven balance to equal-allocation pushes by collisions all another particles a little out of their previous directions (Fig.11):