1.5 The surch of the structure for electron and proton
Hitherto are the particles characterize so: They are all identical, moved with velocity of light, reflect each other and therefore they can build structures. Their middle distance in the space is 6.4597 10-12m.
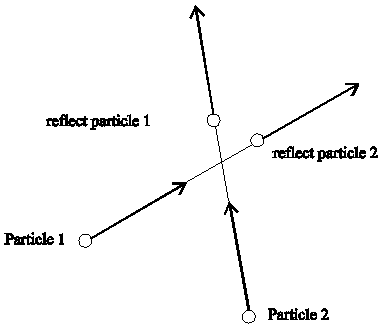
Now is the question, how form the particle for example an electron ore a proton? How they form a photon was say before. To the building of a structure are needed collisions of particle. If collide only two particle, then they reflect each other as two billiard-balls (Fig. 1.5-1).
Fig. 1.5-1: Collision of two particles
The result is the same, if two particle each other cross. They are not different anyway. Another is a collision of three particle (Three-collision) (Fig. 1.5-2).
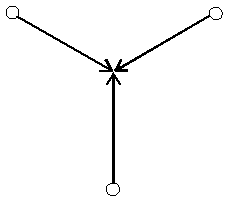
Fig. 1.5-2: Collision of three particles in a plane and in a angle of 120°
Here can build a flat structure for example from hexagons (Fig. 1.5-3).
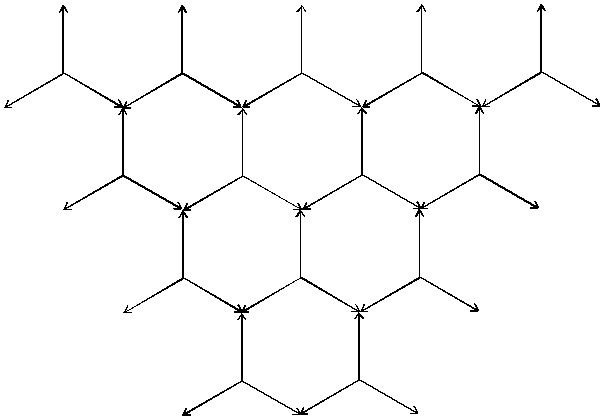
Fig. 1.5-3: Hexagon-structure
The particle meet in the moment at the point of the arrows and then they flay back.
Make four particles a collision, than are possible three-dimensional structures, see tetrahedrons in Fig. 1.2-3.
By the principle “What is possible, that come; it is only a question of time” can exist that structures.
To the building of a structure by collision of three or four particles stay in the face of destructed proceedings. Exist two destruct- proceedings:
1. The outermost particles flay simple off, because they have not partners for reflection.
2. Also inside particles in the structure can fling out there course by a 3-particle-collision. (Natural in counter-move can results on this way a „repair “ in the inside of the structure.)
The structure are likely very dynamic, that is synthesized and destructed. They stand in a balance with its background by a continue exchange of particles.
Because is nothing known about the structure of electron and proton on the basic of particles, are to take assumptions next to. If the assumptions not give good results, then must new think.
A simple atom, be made of a proton and an electron, the hydrogen, has in the cosmos the 3K-radiation round it or as figure with particles: criss-cross flying particles. The proton has inside likely a spatial structure. For the electron between proton and space are likely plane structures for assumptions. The particles of the round space can see as „linear structure” (line of fly).
The proton has likely a structure of a tetrahedron, the electron a structure of a hexagon.
1.6 Probability of a 3-particle-collision
Because as for the form and as for the decomposition of structures is need a 3-particle-collision, shall before the calculations of examination here investigate, what is the middle length of way for a particle to a 3-particle-collision. The conditions of a 3-particle-collision are:
1. The three particle has a definitely direction, who aim at the point of meet.
2. The three particle are equal distant from the point of meet( have defined distance to the point of meet).
For the comparison the conditions for a photon:
1. The three particle has a definitely direction (in these case the same direction).
2. The three particle has defined distances for each.
The conditions for a
3-particle-collision and for a photon are on principle se same. Because are
conduct the investigations on a photon, very well at the most representative
photon, that with the length of wave
(see Fig. 1.6-1).
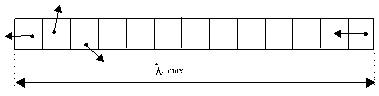
Fig. 1.6-1: Part of the cosmos with the
first particle and the last particle of a photon with the length of wave
In fig. 1.6-1 is to see the first
particle of a photon in the first cube of a part of the cosmos. Additional
particle of the cosmos follow in the next cubes. The middle distance of the
particles, hence the edge of the cube, is ∆λ∆n=1
.On the end of the part is the last particle of the photon. (The third particle
of the photon is not shown.) If go from the first particle in the next cube and
ask:”Are you the last particle of these photon?”, then is the answer: “no”. This
repeats to the last cube. Need hence
/∆λ∆n=1
trial, to find the last particle, or another, to fill the above conditions of a
photon. The number of hits connect with trials is the belonging to probability
p. The probability of a 3-particle-collision (p3) is therefore:
p3 =
1.6-1
A trial is here a step of the length ∆λ∆n=1 , therefore the middle distance of two particles in the space.
If market p particle 1 the probability, that particle 1 fill the condition of direction and distance and corresponding p particle 2 for particle 2 and p particle3 for particle 3, then is the probability of a 3-particle-collision:
1.6-2
In this connection consider to the destruction of a structure by a 3-particle-collision:
With the exist of a structure exist the directions of the particles of the structure too. To a destruction must only two “strange” particle collide with the particle of the structure, before it reach the meeting point (Fig. 1.6-2):
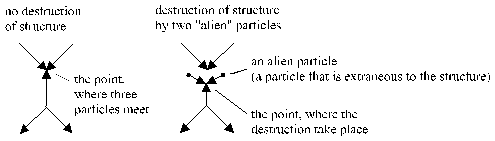
Fig. 1.6-2: Destruction of a structure
For these must fill: An extraneous particle has an appointed direction and an appointed distance to the point of disturbing and a second extraneous particle has an appointed direction and an appointed distance to the point of disturbing too.
With that valid for the destruction:
1.6-3
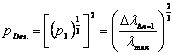1.6-4