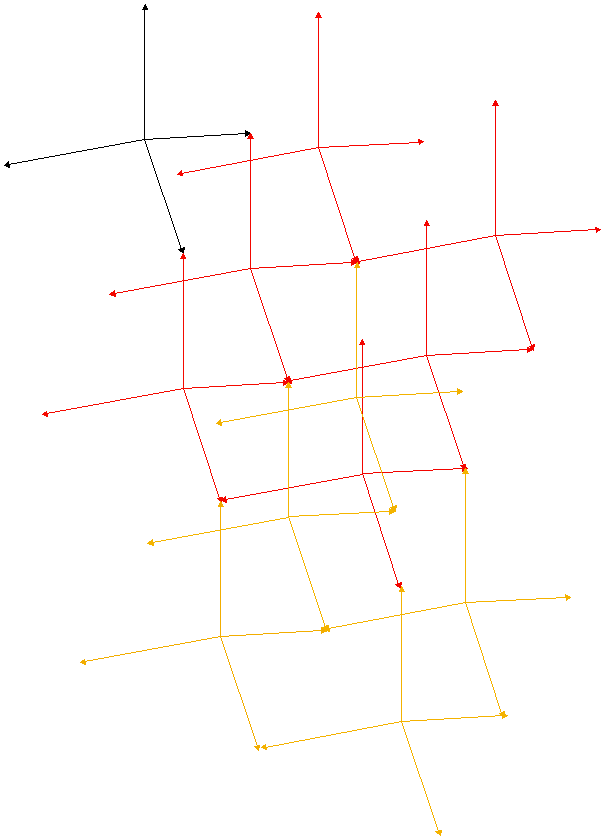
2.2 Connection of the 3K-radiation and the mass of the proton
After the calculation with this structure of the electron yield a workable result and in these calculation is anchor the structure of a proton, make an effort to estimate the mass of the proton from these structure. As structure was assumed a dynamical accumulation of tetrahedrons of 4-particle-collisions as to see in fig. 2.2-1 and as to see in fig. 1.2-3 as a three-dimensional structure based on 4-particle collision.
Fig. 2.2-1:
Structure of a proton, formed from tetrahedrons (The colors are relate to the
planes of layer of tetrahedrons). Respectively four particles are in the center
of the tetrahedrons and fly along the arrow to the next meeting-point. By it is
the distance of two particles in medium
, logically the same as in the
3K-space.
The number
of particles, which take part on
the proton, is here as at the electron limited by the largeness of the
structure, where can build to the destruction by a 3-particle-collision:
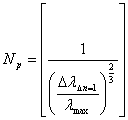2.2-1
A
(minimal group of energy) are to
see as three particles,
follow result the number of
as
.
2.2-2
Now is still to estimate the length of
wave 
of these
:
From the presentation of a
4-particle-collision in fig. 2.2-1, specified in the following fig. 2.2-2, is
deduced, how long is the distance between two consecutive particles, where are
free because a destruction of the structure, i.e. not are reflected and fly on
the same line in the same direction and also are a
. The third particle appertaining
to is from these structure too and is
integrate within these . It is here not searched, for it is
coming from these structure, than it can back in the structure and is find
there.
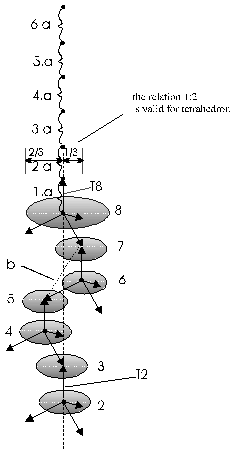
Fig. 2.2-2: Exit of the start-particle (T8) and of the end-particle (T2) from the structure
Explanation of the fig. 2.2-2:
Point of start is the knot in plane 8, from these just the four particle diverge, including T8.
In the first step cover particle T8 the distance “a”.
An another particle fly to the knot in plane 7.
Particle T8 is after the first distance “a” not reflected, because on these place the structure is destroyed. It fly wider.
The first step is ended with the reflection in knot of plane 7.
Now begin the second step. From knot in plane 7 fly a particle to the knot in plane 6 and another particle to the knot in plane 8. T8 cover its 2. distance „a“. The second step is to end with the reflection in knot in plane 6. But the particle, what is fly in the direction to plane 8, is not reflected, with that is the knot in plane 7 destructed too.
In the third step cover T8 its 3. distance “a” and from knot in plane 6 arrive one particle at the knot in plane 5 and another particle at the knot in plane 7.
Because these is destructed, are not a reflection and with that is the knot in plane 6 destructed too.
The third step end with the reflection at the knot in plane 5.
In the fourth step cover T8 its 4. distance “a” and from knot 5 arrive one particle to knot in plane 4 and another particle to knot in plane 6, where not is a reflection and with that is the knot in plane 5 destructed too.
The fourth step end with the reflection in knot in plane 4.
In the fifth step cover T8 its 5. distance “a” and from knot in plane 4 arrive one particle to the knot in plane 3 and another particle to the knot in plane 5, where not is a reflection and with that is the knot in plane 4 destructed too.
The fifth step end with the reflection in knot in plane 3.
In the sixth step cover T8 its 6. distance “a” and from knot in plane 3 arrive one particle to the knot in plane 2 and another particle to the knot in plane 4, where not is a reflection and with that is the knot in plane 3 destructed too.
The sixth step end with the reflection in knot in plane 2.
With that the particle T2 start its flight in the same direction as particle T8.
Its remainder to them is above
additional the distance of the
structure between plane 8 and plane 2. It is:
The distance between T8 and T2 and with
that is also:
.
2.2-3
Now it is necessary to determine “a”. The spatial extension of the structure connected certainly with the middle distance of two particles in the cosmos.
The distance a shall therefore estimated
from the middle distance of two particles
. Here is assumed, that be valid
for the structure of a proton the middle distance
of particle too.
In the structure above (Fig. 2.2-1) moved the particles from one knot of meet by the distance “a” to the next knot of meet and back (Fig. 2.2-3).
Fig. 2.2-3: Particles moved to a knot of a tetrahedron, there is here mutual distance 0 (nearly).
(A marked particle meet in a knot three particles, after its flight back then meet with three another particles.)
How is to estimate the distance a, if
the middle distance of the particles shall
and the particles fly to and from
the knots? In the knots they have nearly the distance 0 one with another, in
moving from knot grow the distance and at the moving to the another knot the
distance reduced and final it is (nearly) 0 anew. Because the particles fly from
knot and back, they removed the first distance a/2 and they neared in the second
distance a/2 each other. They have consequently at a/2 the maximal distance each
other. This maximal distance signet as “x”. It is to see in fig. 2.2-4.
Fig. 2.2-4 Construction of the maximal distance of two particles each other.
From the triangle ABC in fig. 2.2-4 result on base of resemblance at triangles:
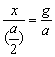2.2-4
and from these the maximal distance x:
2.2-5
(Note: In the carrying out of 2003 was falsely assumed the maximal distance as g and not as g/2).
The middle distance is therefore between
0 in the meeting point and the maximal distance
at a/2.
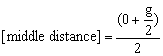2.2-6
In a tetrahedron is the distance g:
2.2-7
With that follow:
2.2-8
As above assumed, shall be valid for the
structure of a proton the middle distance
for particles too.
With
2.2-9
follow
2.2-10
and after shifting
2.2-11
With that is a calculable.
Now can from equation above
calculate the
.
2.2-12
2.2-13
With that follow from
2.2-14
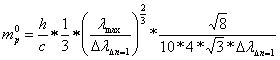2.2-15
mp0=1.637*10-27 kg instead of 1.673*10-27 kg; deviation: -2.15%
2.2-16
Here lead the correction of λmax (and therefore ∆λ∆n=1 too) as at the electron too and the correction for the [middle distance] in the structure of the tetrahedron of the proton to a distinct improvement of the exactness in front to the results of 2003. As was the deviation in 2003 at +33%.