2.6.2 Constant of magnetic field

Although the constant of magnetic field μ₀ is calculable from ε₀ and c, shall here take place a derivation as for ε₀ . The constant of magnetic field is according to /2-11/:

                                                                  2.6.2-1

Here shall these number derived from the 3K-radiation. Starting-point is as at ε₀ once more a low of force, and that the force F between two parallel conductors of current with distance r and length l.

                                                                   2.6.2-2

                                                                   2.6.2-3

As at ε₀ shall here the force F estimate on the base 3K-radiation and from the same formula as at ε₀ :

                                                                        2.6.2-4

Mean from the per unit of time active number of photons  with here energy  respectively  .The currents I₁ and I₂ shall identical and flow with velocity of light. They can replace by flowing charges.

                                                                                2.6.2-5

The current shall so big, that in the time τ only one charge is flowed. The time τ shall

                                                                                                                     2.6.2-6

are, where in sequence for ∆λ every is mean ∆λ_∆n=1 . Than is

                                              2.6.2-7

To that belong to Fig. 2.6.2-1 for the both wire.

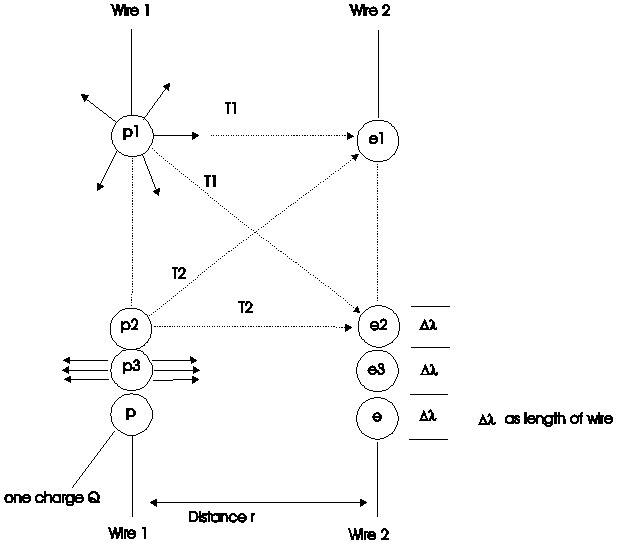
Fig.2.6.2-1: Fly of particles at the wires

As at ε₀ the particle fly from proton ball-shaped in all directions of space (shown at p₁). As at ε₀ shall here to an electron the recipient. Because the effect of the particles T₂ on e₁ is the same as the effect from T₁ on e₁, can assign each e_i the particles of his p_i (shown at p₃). During therefore at ε₀ the particles remove from p by a sphere, can here see a disk (a pressed sphere) as model. As at ε₀  is the area of target  for a particle. The part of appropriate proton-particles to all particles, who start from proton, is with this at the area of target  to the complete possible area of  .

                                                                  2.6.2-8

                                                                  2.6.2-9

With that is

                                  2.6.2-10

                                                      2.6.2-11

The length of wire l can select throughout to . For  is as at ε₀ the term  of the proton to take and for  as at ε₀ the term  with

                                                             2.6.2-12

from chapter 2.2.

                            2.6.2-13

                                                         2.6.2-14

                         2.6.2-15

  instead of 1.25664*10^-6   

                                                                                                                                 2.6.2-16

Deviation: +14.2%

For the connection of ε₀ , μ₀ and c is applicable:

                                                                             2.6.2-17

With the lead here formulas for ε₀ and μ₀ followed:

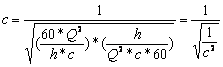                                      2.6.2-18

With this is the connection fulfilled. The deviations of the numbers for ε₀ and μ₀ can only caused by the factor 60. This is estimated by a, that is the length of way of a particle from collision to collision of four particles in the tetrahedron-structure of the proton. Probable is it not only these one number of a, what is tolerate for the construction of tetrahedrons. With only one number of a would be the statistical behavior of particles putting out of low, what is not possible. Precise results for the numbers of ε₀ and μ₀ are expected at all consideration of the statistical distribution.

Next page

List of contents

Back to the start