2.8 Connection of 3K-radiation and send out of light by the hydrogen-atom
The send-out of light by a hydrogen-atom is an interesting connection of proton, electron and light. In these chapter shall derived the connection with the particles. Next is to find a structure of the formula, what is equal constructed as the formula for light, what is send from the hydrogen-atom, for example the Balmer-Rydberg-formula /2-13/:
![]() 2.8-1
2.8-1
Here is R the constant of Rydberg, its number is according to /2-14/:
![]() 2.8-2
2.8-2
Now to the derivation of a such formula.
Take spheres to the sun, in different distances r as showed in figure 2.8-1.

Fig. 2.8-1: Spheres to the sun
The areas of spheres are signed F. Quite can signed the spheres with little letters , for example m and n. From the surface of the sun FS is going a stream of energy. For stationary conditions (is condition number 1) this stream of energy go in identical quantity through the areas Fm and Fn. With that follow the balance:
![]() 2.8-3
2.8-3
Connect the stream of energy with the
respective surface of sphere and signed the stream
![]() , then follow:
, then follow:
![]() 2.8-4, 2.8-5, 2.8-6
2.8-4, 2.8-5, 2.8-6
Of interest is now the difference
![]() :
:
![]() 2.8-7
2.8-7
In the follow development deviate from the model of sun. Instead of sun is used a center (Fig. 2.8-2).
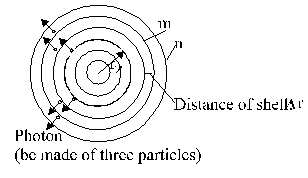
Fig. 2.8-2: Spheres to a center
From these center go a number of
photons, signed as effective photons
![]() . For these photons are effective
the equation derived above too. Just so from here shall used beside the
stationary condition (above the condition 1) the another three conditions.
. For these photons are effective
the equation derived above too. Just so from here shall used beside the
stationary condition (above the condition 1) the another three conditions.
Condition 2: The stream of energy are
only photons with one length of wave
![]() .(Here shall x1 mean, that these
value is the unknown quantity number 1 ).
.(Here shall x1 mean, that these
value is the unknown quantity number 1 ).
Condition 3: The distance of the spheres
is regular ![]() .
.
Condition 4: The radius of the center is
subdivided with ![]() equal the radius of the spheres.
equal the radius of the spheres.
May be z sections:
![]() 2.8-8
2.8-8
The from center going effective energy
![]() (in the sun-model
(in the sun-model
![]() ) can signed as a number
) can signed as a number
![]() of photons with a wave-length
of photons with a wave-length
![]() .
.
![]() 2.8-9
2.8-9
Moreover can signed the radius r as
multiple of ![]() . The multiple are m and n:
. The multiple are m and n:
![]() 2.8-10, 2.8-11
2.8-10, 2.8-11
With that follow
![]() 2.8-12
2.8-12
From
![]() follow
2.8-13
follow
2.8-13
![]() 2.8-14
2.8-14
and with that
![]() 2.8-15
2.8-15
Now is to free the left side of the
equation from area- and time-relation. These is to make by multiplication with
the still unknown area ![]() and the unknown tim
and the unknown tim
![]() .
.
![]() 2.8-16
2.8-16
The difference of energy
![]() correspond an equivalent
correspond an equivalent
![]() :
:
![]() 2.8-17
2.8-17
Then follow:
![]() 2.8-18
2.8-18
These is the searched structure of the formula of Balmer-Rydberg, where the mentioned 4 conditions are adhere to.
Now is from the center to go to the proton and to estimate the three unknown terms.
For hydrogen is z=1. Follow from condition 4 is:
![]() 2.8-19
2.8-19
That mean, the radius
![]() of the source is equal the distance
of the spheres
of the source is equal the distance
of the spheres ![]() .
.
Then follow
![]() 2.8-20
2.8-20
That is the structure of the above given Balmer-Rydberg-equation. The term in the angular bracket must logical it equal the Rydberg-constant R .
Now are to estimate the terms in the angular bracket.
Estimation of
![]() : From the proton are send
according to chapter 2.6.1 (Fig. 2.6.1-1) the number
: From the proton are send
according to chapter 2.6.1 (Fig. 2.6.1-1) the number
![]() of photons with the wave-length
of photons with the wave-length
![]() . But not all of these photons can
be effective at the generation of a photon with the searched wave-length
λ . From the lot of particles, flying from the proton, can
build with an another particle only then a λ , if
these needed third particle has the right distance λ
and the right direction (Fig. 2.1.2-3). In chapter 2.1.2 was found, that the
probability of a particle, to have an estimated distance and an estimated
direction in relation to an another particle is p1 . With
. But not all of these photons can
be effective at the generation of a photon with the searched wave-length
λ . From the lot of particles, flying from the proton, can
build with an another particle only then a λ , if
these needed third particle has the right distance λ
and the right direction (Fig. 2.1.2-3). In chapter 2.1.2 was found, that the
probability of a particle, to have an estimated distance and an estimated
direction in relation to an another particle is p1 . With
![]() 2.8-21
2.8-21
follow ![]() 2.8-22
2.8-22
and with
![]() correspond to chapter 2.6.1 than:
2.8-23
correspond to chapter 2.6.1 than:
2.8-23
![]() 2.8-24
2.8-24
(For simplification is set here and in
the follow progress ![]() .)
.)
Estimation of
![]() :
:
The wave-length of the from center proton emitted photons is λp . In chapter 2.2 was
![]() 2.8-25
2.8-25
estimated.
Estimation of
![]() :
:
The emitter-area
![]() is the sphere of the center:
is the sphere of the center:
![]() 2.8-26
2.8-26
Estimation of
![]() :
:
The interval of time for the emergence of particles from the proton was derived in chapter 2.6.1 as
![]() 2.8-27
2.8-27
Now can calculated the term in the angular bracket.
 2.8-28
2.8-28
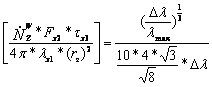 2.8-29
2.8-29
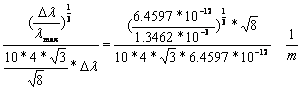 2.8-30
2.8-30
![]() 2.8-31
2.8-31
Deviation: -2.8%
Although the number is in good agreement with the Rydberg-constant, the derivation of the formula is more speculative than logical. The ground is the at present insufficient clearness of the structure and function of the electron on the base of the particles (Betome).