3.12 Theory of relativity and particles
3.12.1 General difference of theory of relativity and description of the nature by particles
The general difference between theory of relativity (TR) and the description of nature by particles is to form an idea for the time. The time take in the TR the same role as another physical terms (space, volume). At the particles has the time generally not any role. The time is based only at individuals, where have a capacity for memory. For all other exist not a time, only a spatial coordination.
3.12.2 The specific theory of relativity and particles
The specific theory of relativity (STR) operate at the relativity in absence of gravitation /3-10/ and acceleration. It are steady motions. At the example of the extension of time in the STR shall test here, to find the connection to the particles.
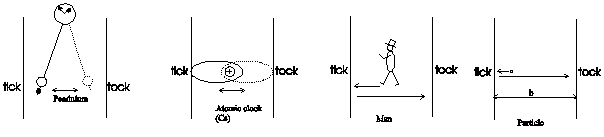
In fig. 3.12.2-1 are to see four clocks.

Fig. 3.12.2-1: Different clocks ( The points of return for the particles are the meeting-points in the tetrahedrons).
The first is a pendulum clock, what at the touch on the left line say “tick” and on the right side say “tack”. The second is an atomic-clock, where oscillation to left end with “tick” to and its oscillation to right with “tock”. The third clock take the part of your self, by go from the right side of a street to the left and beck. At the fourth clock take over these role a particle. These clocks not moved in the space, they repose for example in a lab (index L). The distance between the lines of bounds is b. The particle in the fourth clock is moved with velocity of light c, as say in chapter 1.1.2 for particles. Than is the time for the flying of the particle from one bound to the other bound:
![]() 3.12.2-1
3.12.2-1
Now to the clocks in motion. For these take the bounds left and right as bounds of a street (Fig. 3.12.2-2) and the direction for move shall up.

Fig. 3.12.2-2: Different clocks in motion
For the particle are signet the distances a and d additional to b. In these triangle is:
![]() 3.12.2-2
3.12.2-2
The distance a cover the particle in the time tmov (mov for moved). In the same time the particle moved forward the distance d on the “street”. With that the particle has on the street the velocity
![]() 3.12.2-3
3.12.2-3
in direction of the street, although it fly with velocity of light c. For the distance a is:
![]() .
3.12.2-4
.
3.12.2-4
With that are connect the distances a, b and d with times and can take place in the equation above:
![]() 3.12.2-5
3.12.2-5
ore changed:
![]() 3.12.2-6
3.12.2-6
and further:
![]() 3.12.2-7
3.12.2-7
and finaly:
![]() 3.12.2-8
3.12.2-8
But these is the equation from the specific theory of relativity for the expansion of the time, the times of not moved (Index L) and moved systems (see /3-11/).
For high velocity v is to see the particle-clock as fig. 3.12.2-3 rough draft a, for velocity of light as rough draft b.

Fig. 3.12.2-3: Particles at high velocity v
In the rough draft b is say indeed “tick”, but not more “tock”. These clock go real very “slow”. Rough draft c present a photon from three particles. The change-over from moved systems to light is not a problem.
Now came the question, whether is better to speak instead of an expansion of time to speak from an another behavior of clocks; and with that general from an another behavior of al moved body in relation to less ore more moved body?
As result of these chapter can follow state:
1. Because the equation for the expansion of time is derived as from the special theory of relativity as from particles to, seem to give no discrepancy between STR and particles.
2. The equation for the expansion of time in the special theory of relativity require at its derivation with particles for mathematics only the theorem of Phytagoras, as in /3-11/ to.
3.12.3 General theory of relativity and particles
The general theory of relativity (GTR) operated with accelerated systems. The behavior of systems is described with the space-time. The space-time is determined by the three coordinates of space and the time, it has consequently four dimensions. In these work is lay open in chapters 3.1 and 3.12.1, that the time as a physical term real not exist, but it is only a product of “creatures with memory”. It is the duty at the clearing of the connection of GTR and particles to present, that the results of the GTR can obtain with the particle-method without the time as the fourth dimension. For these next present the acceleration. In fig. 3.12.2-2 go the man in the same angle from the “bound of street“, as he came, so as he was reflected on a mirror. The same is the case at the particle. In an accelerated system go the man at each touch on the bound in a planer angle from the “street-bound”, mean more in direction of the street (Fig. 3.12.3-1). The same is true for particles. The man and the particle make headway ever faster on the street, logically accelerated.
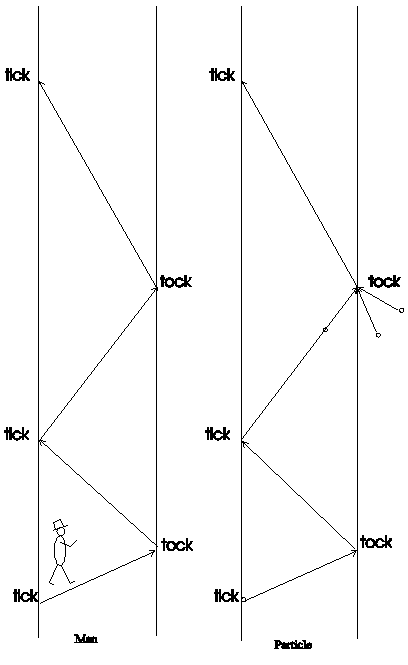
Fig. 3.12.3-1: Accelerated „clocks“
Of interest is now, how is accelerated the particle? The particle but have only two characters:
1. They moved with velocity of light.
2. They reflect another.
From the second character follow, that a change of direction only take place at a collision with two ore more particles. That is illustrated in fig. 3.12.3-2 at a collision.
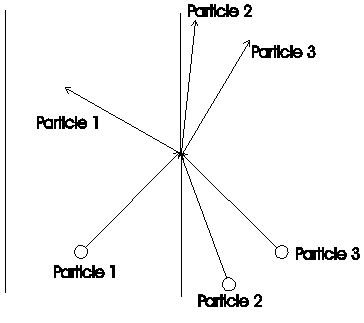
Fig. 3.12.3-2: Refraction of a particle by two another particles (as indicate in fig. 3.12.3-1)
To refract the particle repeated up in direction of the street, must came the collision-particles from bellow ore have a component from bellow. For an acceleration is needed to, that the up-component (in direction of the” street”) of the particle 2 and 3 is the greater , the more up such a collision take place. Such change of the components of direction of the particles was derived before at the refraction of star-light by the sun (chapter 2.5). There was refracted all particles of the 3K-space in direction to the sun, inclusive the star-light. They was more refracted, the more they are near the sun.
Take now at the up-end of the “street” in fig 3.12.3-2 a sun, than are all particles and consequently the particle 2 and 3 refracted in direction to the sun. They obtain an ever bigger component in direction of the “street”, to near they are at the sun. That is exact the demand of the above underlined sentence. An acceleration take that, where emitted particles (particles as photons) from an existing structure (sun be made off protons and electrons). This is known as gravitation of a mass.
With that is interpreted the mode of action of particles at the acceleration.
Now back to GTR at the example of an accelerated and a non-accelerated clock (Fig. 3.12.3-3).
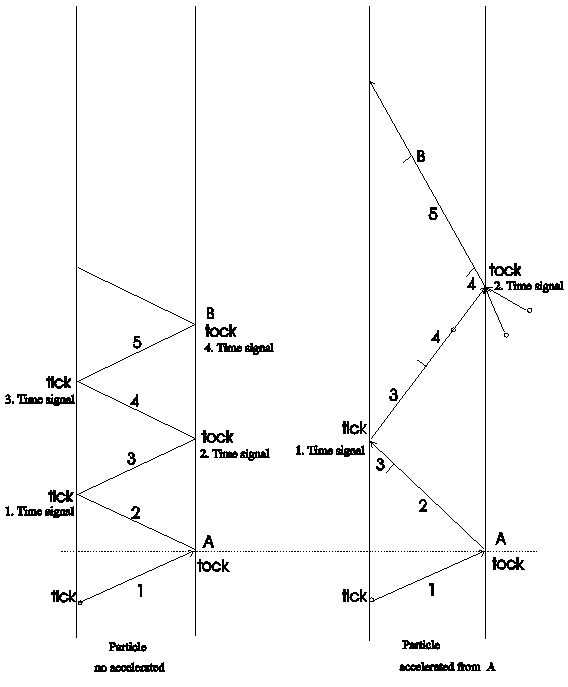
Fig. 3.12.3-3: Non-accelerated and accelerated clock
The non-accelerated clock correspond fig. 3.12.2-2, the accelerated clock fig. 3.12.3-1. Up to point A go both clocks identical, from there is the one clock accelerated. The comparison of the clocks is to end at point B, there has run both particle-clocks the same distance (5 sections with velocity of light).
During the non-accelerated clock from point A to point B send four signals of time (tick ore tock), send the accelerated clock only two signals. We would say, the time at acceleration run slowly.
But these is the same result, at find the GTR for these case. So cite in /3-12/ relating to a formula: “The physical content of the formula is the follow: Given two identical constructed, synchronous clocks, to begin in rest relative to each other. If one is for an fixed time-distance in a field of gravitation, than the two clocks not more synchronous, but the clock, was in the field, is delayed.” (The rest relative to each other is see up to point A in fig. 3.12.3-3, the fixed time-distance is the action from A to B.)
At these comparison of clocks in fig. 3.12.3-3 are only used distances of lengths, somebody times are not needed.
With that is demonstrated, that results of GTR can derived with the particle-method. A contradiction between GTR and particle-method seem not exist. With only three dimensions (the three space-dimensions) is the particle-method but more simple in relation to the GTR with four dimensions.
3.13 Standard type of the physics of the basic-particles and particles
(Betoms)
These chapter shall show the simplicity of the particle-type (Betoms) in relation to the standard-type of the physics of the basic-particles. Here take action basic-particle, forces and gravitation.
Basic-particle:
In accordance with /3-13/ is the standard-type of the physics of basic-particles described follow: “With these type can lead beck all matter our world ultimately to only twelve different sorts of basic-particles: the electron and two near related particles, three sorts of electrical non- load particles, named neutrinos and six sorts so-called quarks.” During exist in the standard-type twelve different particles, exist in the betom-type only one particle. At the twelve basic-particles of the standard-type exist a lot off characters (for example charge, mass, interaction with other particles and more). The particle (betom) has only two characters:
1. It moved with velocity of light
2. The particles reflect each other.
Forces:
At the standard-type exist by particles forces too. In accordance with /3-13/: “Between the matter-particles work three basic-forces: the electro-magnetic force, that particle is the photon; the so-called weak nucleus-force, what make estimate radioactive disintegration and work in three different particles and the large nucleus-force, what effect the connection of the nucleus and is given by 8 so-called gluons.”
In the betom-type no exist forces.
Gravitation:
In accordance with /3-10/ quotation:“-the standard-type is formulate on the base of Special Theory of Relativity, therefore in a flat, gravitation-free space-time.”
As describe in chapter 3.12.3 at GTR and show in chapter 2.3 at the derivation of the gravitation-constant and in chapter 2.5 at the diffraction of light at the sun too, is the betom-type usable at the gravitation.
The make explanation in the comparison of standard-type and particle-type (betom-type) demonstrate, that in the particle-type is a large potential for development.