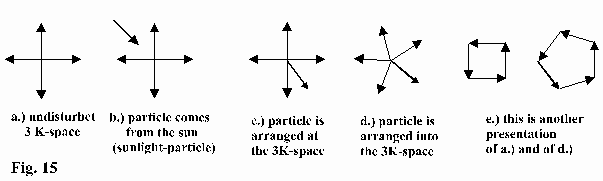
5.2 Application of the theory to the deflection of a ray of light when passing the sun
5.2.1 Aim
It is known from measurements and calculations that a ray of light flying close by the sun is deflected in direction to the sun. The angle of deflection is 1.75" regarded from the earth.
It is the aim to calculate this value from the described theory above.
5.2.2 Proposal for a model
By collisons of at least three particles corresponding to the theory in chapter 4 particles coming from the sun with information of the sun set into reciprocal action with the light-ray-particles coming from a star with information of a star.The effect of the sun-rays at the star-ray can be derived on the basis of the 3 K-space:
Indeed the star-ray has also an effect on the 3 K-space because it disturbs the 3 K-space. But the effect of the sun-rays is much higher because much more rays are close to the sun. Therefore, the particles of star-rays are regarded as 3 K-space-particles:
The mode of action is demonstrated in Fig. 15: The sun-light-particle get to space with a certain arrangement. By these collisons this arrangement will be changed. The arrangement strives for another state. In this state the sun-light-particle will be entirely integrated.
(Remark: The representation refers to a plane, in reality it is to be regarded as a sphere)
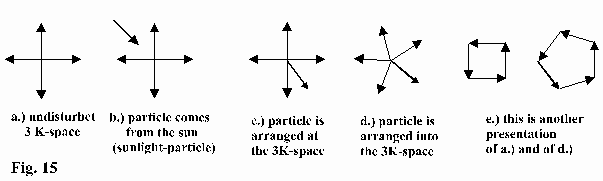
The entered and integrated sun-particle changes the direction of the existing 3 K-particles. It happens trough 3-particle-collisions (Fig. 15 d). Finally, a complete equalization will be achieved. All other 3 K-space-particles get a direction-component that deviates the 3 K-space-particles from the sun-particle. The sum of these direction-components corresponds to the direction-component of the entered sun-particle (the complete equalization is shown in Fig.15e).