5.2.3 Interpretation by formulas
If the value of the direction-vector of the sun-particle is 1, then each
![]() -particle will get a vector of
change of direction of
-particle will get a vector of
change of direction of
![]() , for example in a considered
space of 1 m3.
, for example in a considered
space of 1 m3.
This fact is caused by the single sun-light-particle.
The direction changes for all particles in this volume of 1m3 to the sun (Fig.15d).
Whereas the value
![]() is to be
determined as: N1m3
=
is to be
determined as: N1m3
=
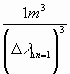
This vector of change of direction causes the angle of change
![]() .
.
Presentation for one sun-light-particle in figure 16 (whereas the abbreviation " S-particle" for a sun-light-particle is used):
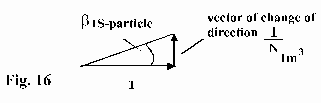
By using this drawing, the angle of deflection
![]() can be calculated. A 3K-particle as
well as the star-light-particle is deflected by this angel when one
sun-light-particle enters the regarded volume of 1m3.
can be calculated. A 3K-particle as
well as the star-light-particle is deflected by this angel when one
sun-light-particle enters the regarded volume of 1m3.
![]() =
=
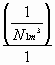 ;
;
![]() =
arctan
=
arctan![]()
The deflection takes place on a determined stretch of way of the star-light-particle.
The volume of 1m3 is considered to be a cube. It is arranged that
the star-light hits a plane vertcally. The distance covered by the
star-ray-particle on which the deflection
![]() takes place has consequently the length of 1m.
takes place has consequently the length of 1m.
The deflection of the star-light on passing a distance of 1m caused by one sun-light-particle is as follows:
![]() =
=
![]()
The term above is referred to only one sun-light-particle.
Because of the great number Ns of sun-light-particles in the volume of 1m3, the deflection will be many times higher:

Determination of NS:
A different number of sun-particles is contained in the regarded 1m3-space. This number is dependent on the distance of the sun. The concentration of the sun-light-particles increases on the way of the star-light to the sun. If the star-light gets farer away from the sun, the concentration of the sun-light-particles will decrease. The number of particles Ns coming from the sun per 1m3 and at a distance "r" of the sun can be described as follows:
ds= diameter of the sun and
![]()
The concentration of particles decreases according to the larger spherical surface at the point "r":
![]()
![]() *
*
![]()
The connection of the distance "r" and the stretch of way (n*ds) of the star-light-particles is demonstrated in the following figure 17:
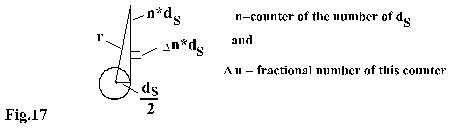
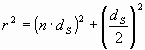
Therefore, the number NS of sun-light particles at a distance "n*ds"of the sun per 1m3 is given by the following equation:
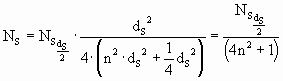
The deflection per 1m of running-length of the star-light can be calculated by using the following equation:
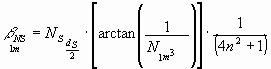
Now follows the calculation for the whole running-length of the star-light (also shown in Fig.17):
The deflection
![]() for a
distance of Dn*ds covered by
a star-ray-particle can be calculated as follows (see also Fig.17):
for a
distance of Dn*ds covered by
a star-ray-particle can be calculated as follows (see also Fig.17):
![]()
![]()
![]()
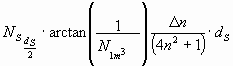
It results from the summation of all Dn of the star (far away: ¥ ) to the sun and the change of Dn to dn the following equation:
![]()
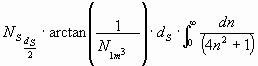
The result of integration is ![]() . The factor
of
approximately 2 is used for the distance of the sun to earth. Therefore,
the wanted angle of deflection a
of the star-light caused by the sun can be calculated as follows:
. The factor
of
approximately 2 is used for the distance of the sun to earth. Therefore,
the wanted angle of deflection a
of the star-light caused by the sun can be calculated as follows:
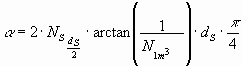

(Remark: The factor 2 can be used because the main reciprocal actions take place close to the sun)