
5.3.2 Attempt to specify the structure of the electron
Considering the equation above the reduction of the number of elements inside the numerator (a part of them) and of the factor of wave-length inside the denominator can be interpreted in this way that different structures of the electron can exist. For this reason I tried to describe the structure of the electron more precisly:
Based on a structure of a 4 particle-collision of the nucleus the electron mediates between the nucleus and the 3°K-space (as shown in Fig.25).

The supporting effect of the electron extends from the nucleus to the destruction by a 3-particle-collision (on average). That is, the supporting effect continues until the particle coming from the nucleus collides with two particles (no nucleus-particles), flying to a determined direction and having a determined distance to it (as shown in Fig.22).
This happens after a number of "Nexperiments" experiments.
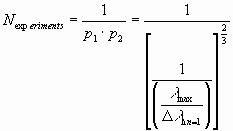
For each experiment a distance of DlDn=1 is required. With that the supporting-length L of the electron can be calculated as follows:
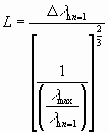
The term "L" can be defined as wave-length of the electron le because this distance also meets the following condition: "particle 1 goes in the marked direction and particle 2 goes in the marked direction and the distance is L".
Now the number ![]() of such
le is still to be determined:
of such
le is still to be determined:
A structure can only be set up till a determined quantity is reached because then a 3-particle-collision destructs the structure.
This happens after a number of Nexperiments resulting from the equation above. The term "Nexperiments" is the number of particles forming the structure. For each le three particles are used. Therefore, the number of particles Nexperiments must be divided by 3 getting the number of le:
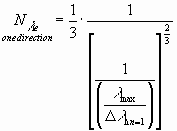
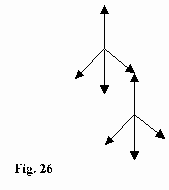
Starting from a 4-particle-structure of the nucleus four directions exist. In each direction a structure (Fig.26) can be built.
Moreover, the following must be noted:
The supporting structure of the electron contains not only particles flying off from the nucleus but also particles directed to the nucleus. This is necessary for the stationary state.
It can not be expected that the nucleus is unchangeably stable and stationary in its structure. It will rather be dynamic and only stationary on average. Therefore, it is to be expected that particles flying in direction to the nucleus also pass through the nucleus.
Considering this, the 4 directions turning outwards are additionally to be added to the 4 directions turning inwards and going trough the nucleus.
Consequently, the figure 8 is to be used for the number of ranges of structure in the calculation:
![]()
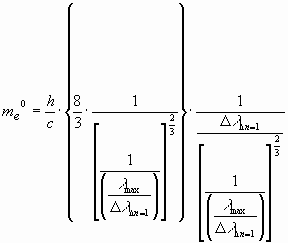
with DlDn=1=7.367*10-12
Finally it can be calculated:
me0=7.995*10-31 kg resp. 9.109*10-31 kg; deviation: -12%