5.4 The structure of the proton
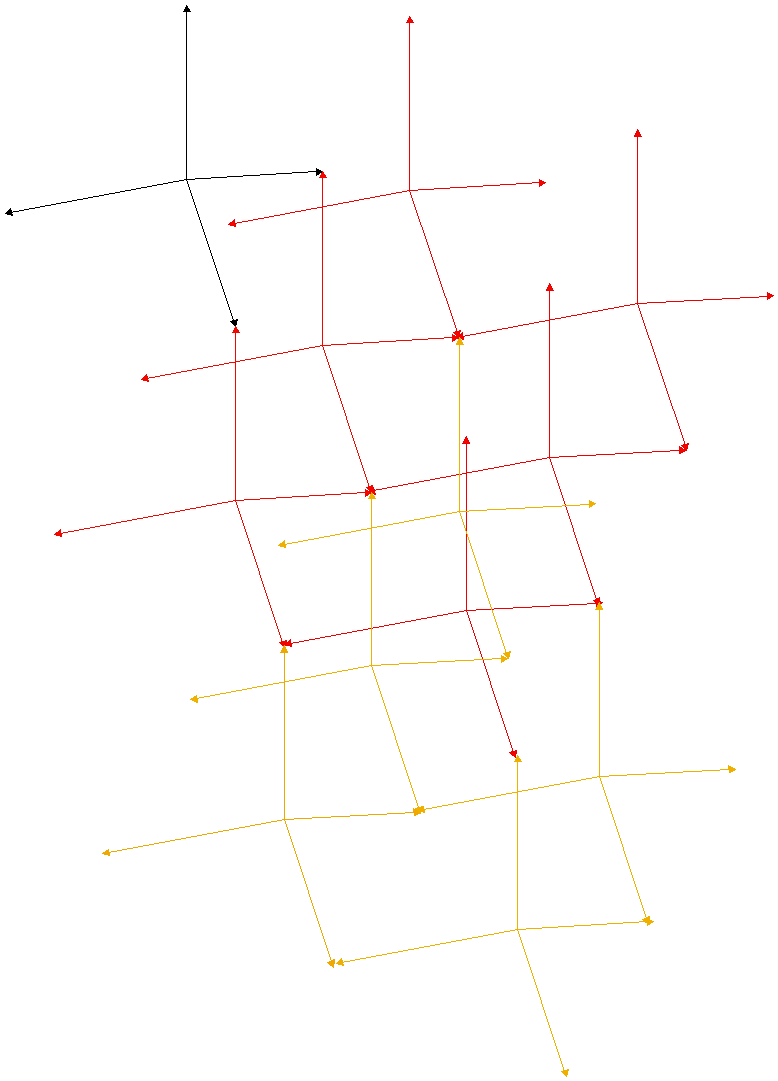
The study of the structure of the electron has produced a useful result. As the structure of the proton is also included in this model, it was tried to determine the mass of the proton considering this structure. This structure was assumed to consist of a dynamical accumulation of 4-collision-tetrahedrons:
This is shown simplified in Fig. 27.

Fig. 27
On average the distance between two particles corresponds to DlDn=1. Therefore it is exactly the same as in the 3-K-space.
The number Np of the concerned particles here is in the same way limited as an electron is limited by the quantity of the structure. This one can be built up until the destruction by a 3-collision:
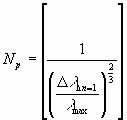
As a l -group (the smallest energy-group) three
particles are in each case considered and therefore the number of
l -groups Nlp results in:
![]()
Now the wave-length of lp of these l -group is to be determined:
The drawing above (Fig 27) of a 4-collision-structure will be specified in figure 28. From figure 28 can be derived how long the distance between two particles is, which will be free due to the destruction of the structure. The term "free" means that these particles will no more be reflected and they are moving in the same direction forming a " l". The third particle forming a part of l originates also from the same structure and it is therefore attached to this l. It will not further be an issue here. If it comes from this structure it can be again arranged to such a structure and it will be found there.
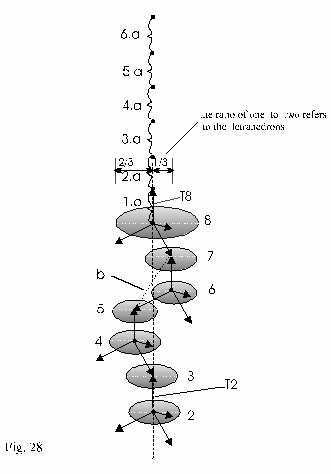
Explanation of the Fig.28:
The starting line is the node on level 8. The four particles including particle T8 are just tending away from this point.
At the first step particle T8 covers the 1st distance "a".
Another particle flies to the node on level 7.
Particle T8 is not reflected again after passing the 1st distance "a" because the structure is destroyed at this point. It flies further.
At the end of the first step a reflection takes place at the node on level 7.
Now the second step begins. One particle flies from the node on level 7 to level 6 and another one to level 8. And our particle T8 covers the 2nd distance "a". The second step is finished by a reflection at the node on level 6. The particle flying in the direction of level 8 can not be reflected. Consequently, the node on level 7 is also destroyed.
At third step particle T8 covers the 3rd distance "a" and one particle moves from the node on level 6 to the node on level 5 and another one to the node on level 7. Because this is destroyed, a reflection does not take place and consequently will be destroyed the node on level 6.
The third step is finished by the reflection at node on level 5.
At the fourth step particle T8 covers the 4th distance "a" and one particle moves from the node on level 5 to the node on level 4 and another one to the node on level 6. At the node on level 6 there is no reflection and the node on level 5 is also destroyed.
The fourth step is finished by the reflection at node on level 4.
At the fifth step particle T8 covers the 5th distance "a" and one particle from the node on level 5 moves to the node on level 3 and another one to the node on level 5. At node 5 does not take place anyway a reflection and therefore the node on level 4 is also destroyed.
The fifth step is finished by the reflection at the node on level 3.
At the sixth step particle T8 covers the 6th distance "a" and one particle from the node on level 3 moves to the node on level 2 and another one to the node on level 4. At node 4 does not take place anyway a reflection and therefore the node on level 3 is also destroyed.
The sixth step is finished by the reflection at the node on level 2.
The particle T2 begins its fly in the same direction as particle T8.
The distance between T2 and T8 is 6*a and additional
the distance of the structure of the level 8 to level 2. This distance is
![]() .
.
The distance between T8 and T2 and corresponding also l p has the value of 10*a.
The distance "a" can be derived from the average distance between two particles DlDn=1.
It is assumed that also for the structure of protons the average distance between particles DlDn=1 is valid.
In the structure above changes the distance between two particles between 0 (on meeting and reflecting at a node) and the distance b. The term b is the distance between the nodes where the particles are coming from. The average distance is calculated as follows:
average distance=
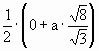
With DlDn=1 = average distance, is
![]()
![]()
and
![]()
![]()
finally the term mp0 can be calculated as follows:
![]()
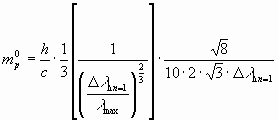
mp0 = 2.226*10-27 kg instead of 1.672*10-27 kg, deviation: 33%