5.5 Constant of gravitation
On the basis of the connection of radiation and mass the constant of gravitation g is calculated. The following formula is used for the defination of g:
For m1 and m2 represents the mass of particles and r is their distance.
The gravitation is determined by means of the change of the impulse. That is the change of the impulse of the arriving radiation, absorbed by the mass m:
gravitation=
with
=rest mass of arriving
radiation
whereas is connected
to the
energy of the arriving radiation:
and Il is consequently:
and
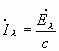with
as radiating power
In the equation above it is set in the term of gravitation:
The term m1 is used for the mass of the electron and the term m2 is used for the mass of the earth. The mass of the electron is used because its structur is compatible with the structure of radiation. The mass of the earth is used because the earth is the basis of the constant of gravitation.
Consequently, the term is the radiating power coming
from the earth and striking the electron. This radiating power has also an
influence on the electron. That means, not the whole radiating power striking
the electron is effective.
From the earth the radiating power
is emitted. The unit of
is W/m2.
The temperature T, however, is not the temperature inside the "hothouse". That means, it is not the temperature of the earth`s atmosphere. In the formula it is to set this temperature, that earth woud have without a "hothouse"-atmosphere. This temperature T has the value of -18°C resp. 255K.
At the distance of "r" from earth, the electron is assumed to be located. Here is the radiating power smaller. This is dependent on the different spherical surfaces. The reducing factor is calculated on the one hand using the radius R0 of earth and on the other hand using the distance r of the electron to the centre of the earth.
The reducing factor is 
The radiating power
in W/m2
arriving at the electron is consequently:
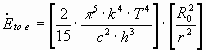
For the determination of the area of absorption that is available for the radiation the diameter of the electron must be used.
If is the diameter of the electron de the area of
circle: will be
.
The radiating power
which is
offered to the electron is consequently:
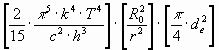
Because the electron has a directed structure, it can only accept radiation. That direction corresponds to the directed structure. In other words, the electron will absorb radiation only in one case: if it "looks" in the direction of the arriving radiation. But it "looks" also in other directions.
The only effective direction from all the other possible directions results
from the area on the assumed spherical surface of the electron that can be
assigned to only one direction relating to the whole spherical surface (like a
marked hexagon on a football). We have learnt from chapter 4 that each
particle and with that also its direction has a volume of
, respectively an area of
, because two particles have a
distance of DlDn=1.
This only direction mentioned above takes up an area of
and the spherical surface is π*de2.
The wanted relation is: 
The "looking" of the electron is dynamical. Whit that only a fraction of the radiation which is offered by the electron is effective. This fraction of radiation corresponds to the ratio of the areas described above.
=
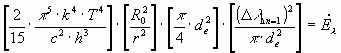
Hence follows
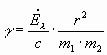
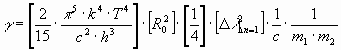
R0=6.378*106 m
m1=9.109*10-31 kg
m2=5.97*1024 kg
Finally the following value is obtained for the constant of gravitation:
