1.3 From structure to distance of the particles of each other

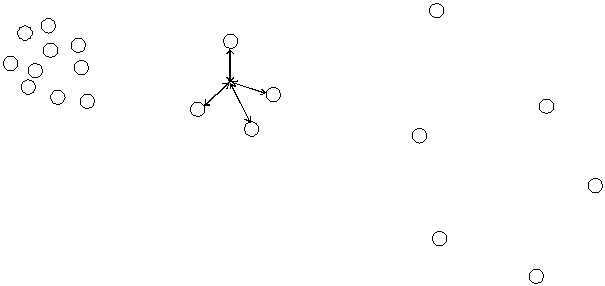
For the bigness of a structure is the distance between the particles, what formed this structure, of significance. During at the photons the characteristic distance of two particles is the length of wave l , confronting us for a three-dimensional structure the question of the distance between the particles complete new. Assuming that the structure of the matter is such tetrahedrons, then is the average distance between two particles in these tetrahedron fundamental for the size of the structure. The distance of the particles in such structure of tetrahedron depend clear from the distance of those particles, how the tetrahedron or the structure do surround (see Fig. 1.3-1).

Fig. 1.3-1: Distance of the particles each other (left are the particle narrower then in the tetrahedron, right are they looser)

What matters is to find these middle distance between two particles in the free, not structured space. Stimulated by the “theory of ether”, after which for example moved the earth trough this ether in the cosmos, I suppose meet the 3K-radiation. The fascination of these radiation is, that it from all directions of the space nearly evenly meet the earth. As an electromagnetic radiation it is too somehow connect with the electron and with that too with the world around us. The particles shall do it too. It was therefore attempt, to find the middle distance of two particles from the 3K-radiation.

1.4 Estimation of the middle distance of two particles from the date of the 3K-radiation

First shall search the middle distance oft two particles in the cosmic space

A cutout of the space is maybe as shown in Fig. 1.4-1.

Fig. 1.4-1: A cutout of the space with particles

The bolts are the directions of move of the particles. Each of the particles belong to in average a certain volume (indicate by the cubes).

What particle is a part of a photon, is from this not clear. A photon correspond Fig. 1.4-2.

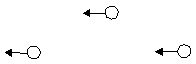
Fig. 1.4-2: Three particles formed a photon (symmetrical and flying in the same direction)

Certainly are find such formation of particles in the space. Even possible to declare, that for each particle can find the two suitable particles. Two photons of the 3K-radiation are to see in Fig. 1.4-3 by start- and end-particle.

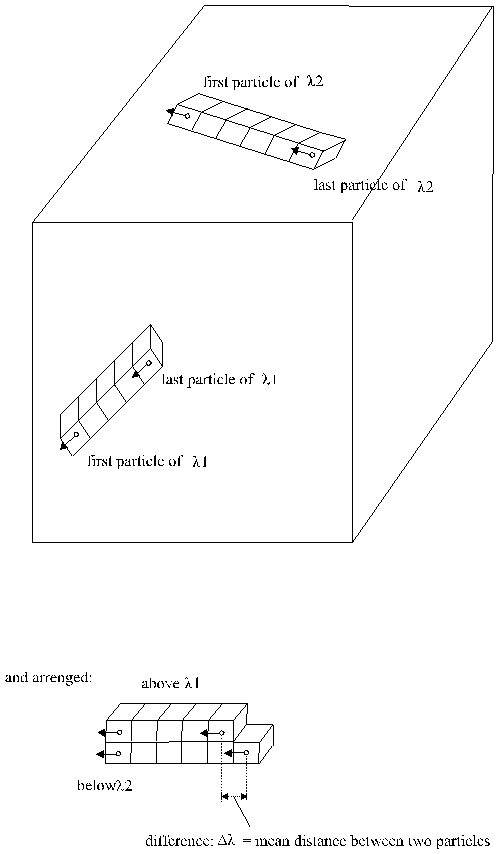
Fig. 1.4-3: Two photons, represent by start- and end-particle

A middle distance of two particles is not to see from the above part of the figure. There is first to put in order (under part of fig. 1.4-3). If place some photons one upon, then follow fig. 1.4-4.

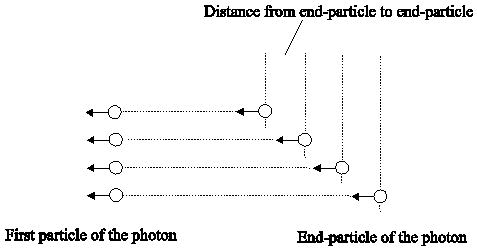
Fig. 1.4-4: Four photons one upon (only start- and end-particles)

The distance from end-particle to end-particle is the wanted distance between two particles, if in middle not an other photon pass between them. Now shall not lay one upon somebody wave-length, but these, who most exist in the 3K-radiation. Think all wave-length from a volume ordered by their length and simplify show by a bolt, then nearly correspond follow Fig. 1.4-5:

Fig. 1.4-5: Photons in particular area of wave-length  (In the center-area was count more photons then in the areas beside it.)

Because exist a limited number of  , is such arrangement possible. In a defined area of wave-length exist especially many of  nearly the same length. This is the area round  , the most numerous photons in the curve of distribution of the electro-magnetic radiation. That is not the area of wave-length with the maximal energy, but the area with the most number of photons. (Note: In the first making out from 2003 page 8 I have apply faulty the maximum of energy.)

In the curve of distribution the photons are sort in small intervals of wave-length. In the area of the most photons exist a lot of photons in one interval of wave-length. The difference of the wave-length is therefore small. For the reason is the middle distance between two particles to such here. If select now one interval in the area of the most photons (Area  )so small, that only one  in it exist (Fig. 1.4-6), than is the difference to the next  exactly the wide of the interval  .

Fig. 1.4-6: The interval of wave-length is select so small, that only one photon within exist.

These interval is the wanted middle distance between two particles (see fig. 1.4-7 and 1.4-8).

To view:

Fig. 1.4-7: Distance of two particles (to see by two photons in the area  )

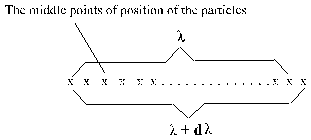
Fig. 1.4-8: Difference of two particles (are shown the start- and end-particle of two photons and between another particle of the space).

After these qualitative estimation of the middle distance between two particles in the space shall now follow the quantitative estimation of the distance.

Calculation of  :

Searched is the necessary interval  , within fitting only one photon. Known is the number of photons per volume in the area of frequency  , estimated for a fixed temperature and of the radiation of a black body:

                                   dn = 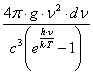                                                                          1.4-1

Because here are differences of interest, is changed from  to l with:

                                                                                                                 1.4-2

                                   dn = 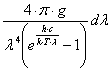                                                                      1.4-3

For an interval of wave-length with only one photon within is valid Dn = 1 (with ∆n as number of photons).

With    Dn = 1             and      Dn =                                                                         1.4-4

result                           1 = 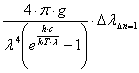                                                                 1.4-5

In these equetion is only ∆λ_∆n=1  unknown. After change result:

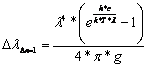                                                                    1.4-6

The value of g is for an in 2 components divisible electro-magnetic wave as 2 to take.

For the quantitative evaluation are T and  to fixed:

For T is to take the value of measurements of the satellite COBE for the 3K-radiation /1-2/:

T = (2.726 0.004)^o K.                                                                                                    1.4-7

In /1-3/ is given 2.725 °K.

For  is to take the most exist wave-length  in the 3K-radiation. It can calculated from the above equation 1.4-3 for the number of photons in an interval of wave-length. The number of photons in an interval is then maximal, if the denominator of the above equation is minimal. To simplify matters are to calculate with a pocket calculator the denominator for different  :

The maximal number of photons exist therefore at the wave-length of λ_max=1.3462 mm.

(Note: In the first publication from 2003 page 8 I have take falsely the maximum of energy from the COBE-measurement at λ_max=1.05 mm.)

With this result the wanted middle distance between two neighboring particles in space:

∆λ_∆n=1 =                1.4-8

∆λ_∆n=1 =6.4597*10^-12 m                                            1.4-9

This value has a fundamental roll for the calculations of example in the next chapters.

Next page

List of contents

Back to the start