2.4.1-1
2.4 Connection between the 3K-radiation and the red-shift
2.4.1 Target
The red-shift is proportional to the Hubble-number. According to /2-8/ is the Hubble-number a constant of nature, who is only known from observation but not from theoretical calculations.
To point at, that can calculated the known number of Hubble, is next to shift the conventional equation:
2.4.1-1
- ∆λLight is the change (shift) of the lenght of wave of the light, the label is only similar to the label for the middle distance between two particles in the cosmos ∆λ∆n=1 .
- H = Hubble-number = 67 km*s-1 *Mpc-1 2.4.1-2 (according to /2-9/)
-
r = length of way in Parsec (
)
2.4.1-3
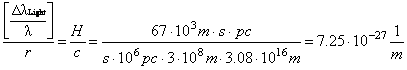2.4.1-4
The value of 
is
now to calculate from a theory, at which the terms
Light
, 
as the length of wave of the light
and r are used corresponding to the left side of equation above.
2.4.2 Model of red-shift
Assumption: Because to reach the 3K-state, are
the lower length of wave than
make longer (red-shift), and the
larger length of wave than make shorter (blue-shift).
Proceedings: By destruction of
the 3-particle-structure of
and regeneration of longer
occur the shift
(see assumption above). Another say: From a photon is one particle from the tree
particles throw out the course and instead of this an another “new” particle in
an another distance to the two “old” particles tie up in the course, the same
take place with a second particle of the photon (Fig. 2.4.2-1).
Destruction and
regeneration are caused by 3-particles-collision. The destruction take place
certainly on an enough long way. The shift (new length of wave) can be
different. Are possible low shifts for example of a part of the middle distance
of two particles in the cosmos, but
very large shifts (to ¥
).
The most build length of wave is certainly that length, who is most existent.
With this is for the
shift 
to take:
.
The new formation is to take here in the squares for the particle 2 and 3 in fig. 2.4.2-1
Presentation:
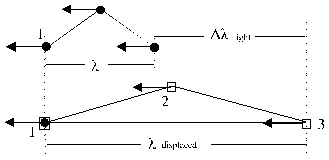
Fig. 2.4.2-1 Change of the length of wave by compensation of two particles of the photon by another particles
Wanted: Length of way r of the light, where has
changed for
(see equation above) ore in other
words: way r, till the particle 2 as well as the particle 3 are in the above
presented positions.
Quantitative estimation: If particle 1 is in the cube above (in Fig. 2.4.2-1 it is shown as a square), must be generated the particle 2 as well as the particle 3 by a 3-particle-collision. Besides they must have the correct direction.
The number of attempts for the generation of the particle 2 is the same number of attempts for one 3-particle-collision in the cube of the particle 2:
During of these attempts has travel
particle 1 the way λmax
. In addition must hit at this generation the correct direction. At a photon has
the last particle the same direction as the first particle. The most often
photon has the length of wave λmax
. Consequently meet the same direction after
attempts. In order to arrival both,
are need therefore 
* attempts. The way of particle 1 is
with that * * λmax
. Just so must take these attempts for the particle 3.
In order to be true generation at
direction as for particle 2 as for particle 3, are need consequently
attempts.
The needed way for
attempts is consequently
2.4.2-1
With that exist for the left part of the
equation above for the calculation of H now
:
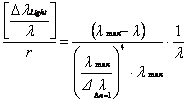
2.4.2-2
In this equation remain a dependence of
the shift from .
With the value of
and
followed for different
from the area of visible light:
for
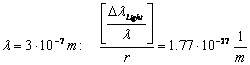instead of (
)
(short-wave-limit of the visible light) 2.4.2-3
for
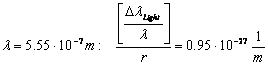
2.4.2-4
(Maximum of
intensity of the sun: about 
;Maximum of the sensitiveness of
the human eye: about 
)
for
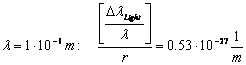
2.4.2-5
(long-wave-limit of the visible light)
Comment: The calculated shift is found in the order of the value of target , but the deviation is comparatively high. The correction of H, λmax and ∆λ∆n=1 lead here in comparison to the value from 2003 a deterioration of the precision. The dependence of the wave-length is unexpected. This fact is further to investigated. (end of comment)
Application to the reach of an information based of light
With the
red-shift on the base above is calculable the reach of an information based of
light. The reach is get to, if the wave-length
has changed by
to the most wave-length
and with that is not different to
the “3 K-noise”.
With that follow from equation above
with 
2.4.2-6
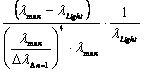2.4.2-7
and final:
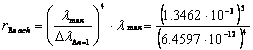2.4.2-8
2.4.2-9
The reach of an information is with that
maximal 
light-years.