2.5 Connection between the 3K-radiation and the deflection of light by the sun
Aim
It is known from measurements and calculations, that a ray of light flying close by the sun is deflected in direction to the sun. The angle of deflection is 1.75” regarded from the earth. It is the aim to calculate this value from the described theory above.
Proposal for a model
Cause of the deflection of the star-light is, that the particles (Betome) of the star-light are deflected by the particles of the 3K-space. These take place by collision of one particle of the star-light with two particles of the space.
But what a cause have the particles of the 3K-space, to change the direction of the particles of the star-light ?
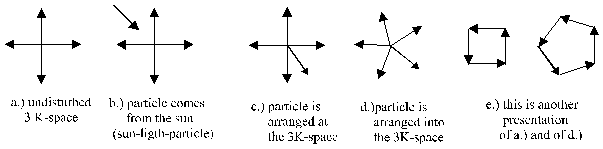
The space-particle moved statistical proportionate in all directions (Fig. 2.5-1a). Coming now particle from the sun, than is the statistical distribution disturbed (Fig. 2.5-1b,c). The regular distribution is restore by collisions of the particles. With that change the particles here direction (Fig. 2.5-1d). Because the direction from the sun is additional occupy, turn off the space-particle from these direction. With that they get a component of direction to the sun. Because the particles of the star-light are not different to the particle of the space, they are influenced same.
Certainly has the star-ray an effect to the 3K-space, it disturbed it, but the effect of the sun-rays is very higher, because near the sun are more sun-rays.

Fig. 2.5-1: Entry of a particle of light from the sun in the 3K-space and its arrange (Remarks: View is 2-dimensional, reality is a sphere. The sum of the direction-components correspond in its value the direction-component of the entered particle from the sun (Compensation, see fig. 2.5-1e: Resulting vector is stay zero.)).
Transformation to formulas
Now it is necessary to transform these conception of a model to formulas.
Estimation of the angle of deflection of one star-light-particle by one sun-light-particle
A space of 1m3, in which are the corresponding number of 3K-particle, is flown trough of one sun-light-particle and of one star-light-particle too.
Is take the
value of the direction-vector of the sun-light-particle to 1 , then get all in
the looked space-volume of 1m3 existing 3K-particles, the one
star-particle too, a part of these value for the compensation of these
additional direction. The vector of the value 1 of the sun-light-particle is
consequently divided to the number of particles in the 1m3 ( Here
number is ![]() ). The vector for change of the
direction has with that the value
). The vector for change of the
direction has with that the value
![]()
as a part from the one sun-light-particle. From the vector of direction of a particle before the action of the sun-light-particle and these vector of change of the direction follow the angle of deflection for the space-particle and for the star-light-particle too, where is caused only by these one sun-light-particle (Fig. 2.5-2).

Fig. 2.5-2: Change of angle β1S- particle of a space-particle by one sun-light-particle (with shortening S-particle for sun-light-particle).
The vector for change of the direction caused consequently the change-angle β1S- particle .
The direction is changed for all 3K-particles and for the star-light-particle too in the 1m3 in the direction to the sun (see fig. 2.5-1d).
The number of 3K-particles N1m3 is to estimate by:
N1m3 =
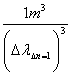 2.5-1
2.5-1
With that is calculable the change-angle β1S- particle ,what get a 3K-particle and a star-light-particle too with the entry of one sun-light-particle in the viewed 1m3 :
![]()
![]() =
=
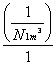 ;
;
![]() = arctan
= arctan![]()
![]() 2.5-2
2.5-2
Now to the length of way for the particle of star-light, where these deflection take place:
Take the viewed 1m3 as a cube and so lay, that the star-light strike vertical on a area. The flowed way of the star-particle, where take place the deflection β1S- particle is with that the length of an edge of cube with 1m3.
The deflection of the star-light during the way 1m und caused by only one sun-light-particle is:
![]() =
=
![]()
![]() 2.5-3
2.5-3
These refer to one sun-light-particle.
Deflection by all exist sun-light-particles in the 1m3
Caused by the number NS of sun-light-particles in the 1m3 (that is the concentration C of the sun-light-particles) is the deflection corresponding multiple:
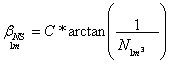 2.5-4
2.5-4
With that can calculated at known concentration of sun-light-particle somewhere in the space the deflection of a star-light-particle for the length of way 1m.
Deflection at the complete length of way
For the estimation of the searched angle of deflection of a star-light-particle during the fly along the sun is calculable for each meter way of fly the respective deflection-angle from the concentration of sun-light-particles on the respective point and at summation (Integration) for the complete flay-way (W) also the complete deflection-angle.
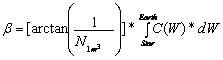 2.5-5
2.5-5
The term arctan is a constant and is depending only from ∆λ∆n=1 .
The integral of the concentration of the sun-light-particles is a conventional problem, not specific for particles.
So far to the conception of the model.
Calculation of this model
Because the calculation is extensive and here disturb the fluency, are the calculation evacuated in a schedule to this chapter.
The result is a deflection-angle 1.64 second of arc instead of known 1.75. These is a deviation of -6.3%.
Remark to the deviation:
In addition to the inaccuracy at the estimation of the concentration of the sun-light-particle in dependence of the distance to the sun can be the distance ∆λ∆n=1 of two particles in the 3K-space a cause for the deviation. If this distance is only 5.6% higher, than result the correct angle 1.75 second of arc. The distance of two particles in the space is calculated only from the maximum, i.e. only from one value of a distribution-curve. At consideration of the statistical totality offer a potential to a better precision.
The up to here in the chapters 2.1-2.5 treated quantitative connections are shown since 2003 in the internet, though with higher deviations (except the red-shift). Because of these not get resonance, I have more connections deduced. They are described in the sequel.
Enclosure A to chapter 2.5: Deflection of light by the sun