2.6.1-2
2.6 Connection between the 3K-radiation and the constants of fields
2.6.1 Constant of the electric field
According to /2-10/ must estimated experimental the electric constant of field.
One get the data ε0 =8.85419*10-12 As/(Vm). 2.6.1-1
Here shall but the value of the constant of the electric field ε0 lead here theoretically from the 3K-radiation.
Derivation of the data of the electric field ε0:
Point of start is the low of Coulomb, what describe the force F of two one against the other influence charges Q:
2.6.1-2
For two appointed charges Q1 and Q2 in a distance r from each other is consequently to deduce the force F from the 3K-radiation, to can calculate the searched constant of electric field ε0:
2.6.1-3
Derivation of the force F:
Force = change of the impulse
2.6.1-4
with
2.6.1-5
Replace of
from
lead to
and consequently to
2.6.1-6 and
2.6.1-7
2.6.1-7
With that is
the per unit of time transferred
energy, transferred by the number
of photons of the wave-length
λ between the charges.
The index w mean, that it is a photon with effect.
With that is
2.6.1-8
and
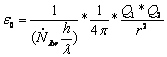2.6.1-9
To estimate from the 3K-radiation are
consequently the number of photons
per unit of time and your length of
wave λ.
For the charges are treated a proton and an electron in the distance r from each other. Proton and electron therefore, because for they already exist characters in connection with the structure by particles. One character of the proton is the flight-out of particles. Because they came from a structure, can such group of particles fly as a formation, for example as a group of 3 particle with the length of the group λp . For illustrate the follow figure 2.6-1-1:
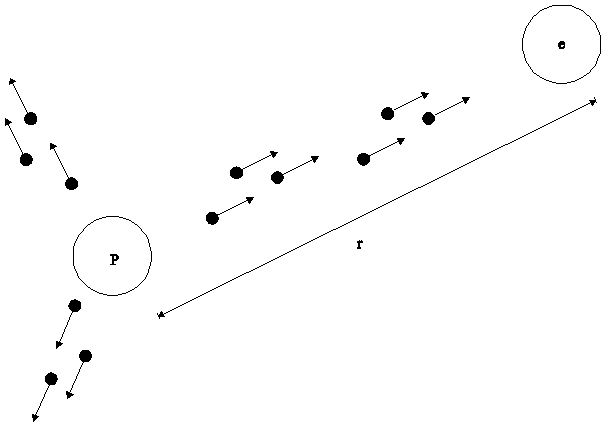
Fig. 2.6.1-1: Particle from proton fly out
Not all of the particle, where fly out
from the proton, have an effect on the electron. Suggest itself, that only these
particle have an effect on the electron, where precise pass in the structure of
the electron, i.e. there meet a particle of the electron. From the 3K-space was
estimated for each particle a volume of
, who it is find. If therefore a
particle coming from the proton want meet the particle in the electron, must it
fly through the area 
to the particle of the electron.
The part apt proton-particles to all particles, where from proton fly out, is
therefore as the area of target
to the area of sphere with the
radius r:
2.6.1-10
Now is to estimate
, therefore the from proton per
second send out photons respective groups of particles. The structure of the
proton was assumed in chapter 2.2 as tetrahedron. The way of the particles from
meeting-point to the next meeting-point was a . Because during the come to of
the particles to the meeting-point in the structure not any particle go away
from the proton, send the proton in these time τ not a
particle.
2.6.1-11
Not before collision of the particles and with that their return of the direction take place the flight-out of the particle from proton (see Fig. 1.2-3).
For the assumption, that after each such
cycle a particle start and with that begin the fly of a 3-particle-group
λp , result the number
such starts 
from the partition of the one
second in the parts τ :
2.6.1-12
The lenght a was in the chapter 2.2 estimated to
2.6.1-13
and λp
also there to 
.
2.6.1-14
If the groups of three particles fly out from the proton, they have the length of group λp ,as was found in chapter 2.2 for the calculation of the mass of proton.
With that are describe all terms for the calculation of ε0 .
2.6.1-15
2.6.1-16
2.6.1-17
The out of the common of these
end-formula is, that not 
is in. The three numbers here in
have their source in geometrical proportions (Tetrahedron) and count up steps
(10) of the length a.
With Q1=Q2=1.60217733*10-19 As/(Vm) followed:
2.6.1-18
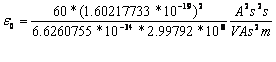
instead
of 8.85419*10-12
2.6.1-19
Deviation: -12.4%
Remark to the deviation:
Here can not the deviation caused by
. Presumable the particles follow
not exact the structure of a tetrahedron.