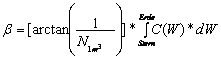2.5-5=A-1
Enclosure A
to chapter 2.5:
ATTENTION!
In this chapter are the numbers in the German notation, mean: 1/10=0,1 not 0.1!
Deflection of light by the sun
The to dissolved equation 2.5-5 was:
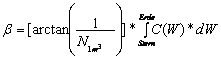2.5-5=A-1
For the number of sun-particles Ns in one cubic metre is here take C as concentration. View we a layer of 1m thickness in distance r from center-point of the sun in fig. A1.
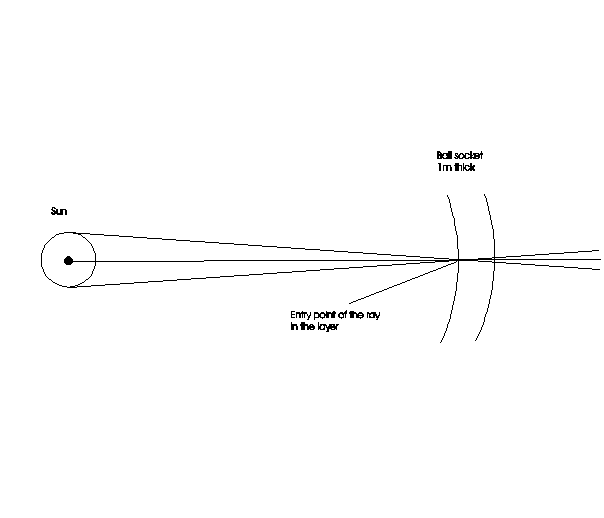
Fig. A1: Layer of 1m thickness in distance r from the center-point of the sun for estimation of the concentration C of sun-particles in these layer
C=(Number of sun-particles/ volume)=(per unit of time in the volume come in number of particles)*(stay-time of the particles in the volume)/ volume A-2
Estimation of the terms in the equation:
„Per unit of time in the volume come in number of particles”:
The per unit of time in the 1m-layer at
r come in particles are at each r exact the from the sun-surface emitted
particles, because on the way not any are disappeared. Named the per unit of
time and unit of area F from the surface of sun (Radius R of the sun) emitted
number of particles as 
, then is the complete from the
sun-surface emitted number of particles
A-3
This is the number of particles, what at r come in the treated volume.
“Stay-time of the particles in the volume”:
The stay-time of a particle result from
the length of way L in the layer divided by the velocity. Because the particle
according to the angle of entry has different length of way L in the layer, is
the stay-time different too (see fig. A1). It is to take an average stay-time
,
result from the average length of way 
:
A-4
„Volume“:
The volume of the layer can estimate for
r>> 1m as 
A-5
With that follow.
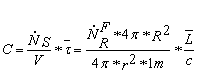A-6
A-7
In these equation is
known by the number of photons from
the surface of the sun (each photon has a determined length of wave λ
and is made of three particles). Now is to find still the average length of way
.
The length of way L depend from the angel of entry (γ) of the particles in the layer , because it named Lγ (Fig. A2).
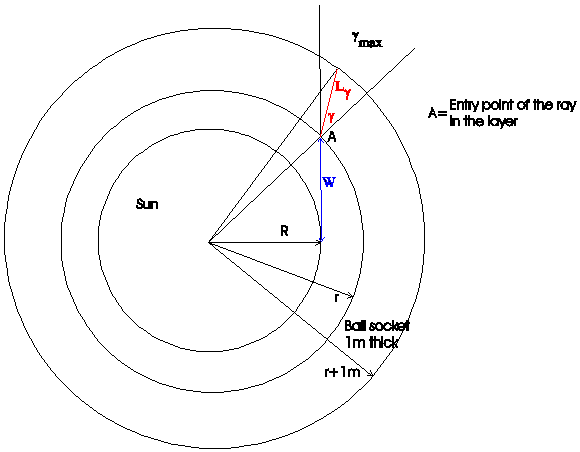
Fig. A2: Estimation of the length of way L of the particles in the layer (For one particle with a entry-angle γ is the length of way Lγ to see).
Is nγ the number of particles with the entry-angle γ , than is the average length of way
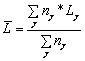A-8
Ore another write:
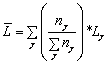A-9
The length of way Lγ is estimable by the cosines-theorem for the entry-angle γ (Fig. A2):
A-10
The change of the equation to Lγ :
A-11
A-12
Because negative L not have sense, follow:
A-13
But now depend not only L from γ , but the number n of particles too, which come in with the angle γ . So come in fig. A3 with the angle γ2 particles from a complete circle at the surface of the sun. During with a angle γ1 only from a little circle and radial even from one point come particles. The most particles come from the largest circle with the entry-angle γmax. (Tangential-rays). They have also the biggest length of way L . (Note: In the calculations at 2003 was used compared to it all rays with the radial length of way 1m. This lead to low stay-times and follow to a low concentration of sun-particles and consequently to a to low deflection of the star-light.)
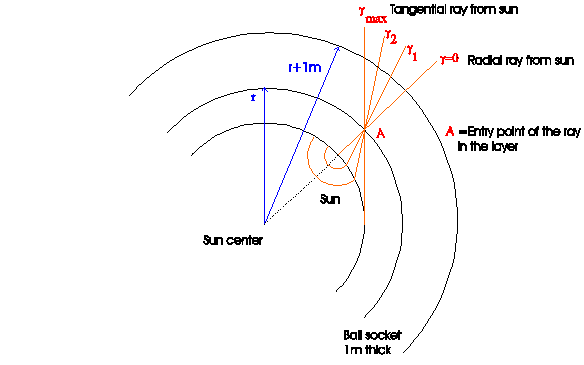
Fig. A3: Circles on the surface of the sun, from where the rays entry in the layer of 1m thickness with the angles γ1 and γ2
For estimation of nγ is coordinated to a little angle-region ∆γ around γ a ring with the breadth ∆b (in fig. A4 δγ respectively db ).
Fig. A4: Breadth db of ring coordinate to the area of angle δγ
The particle, coming in the ring with
the breadth db , are counted nγ . Summation
over all such rings in the range of angles up to γmax
give the total particles 
coming in
With that can the ratio
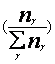express as ratio of the areas
ring-area to circle-area:
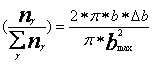A-14
For b can write in accordance with fig. A4:
A-15
The number of bmax depend from the angle γmax and these anew from the distance r of the treated 1m-layer from the sun.
A-16
The equation for
in the layer at the radius r can write :
A-17
From the equation above
follow
A-18
With change from sum to integral follow:
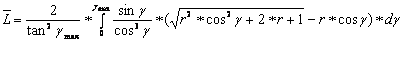A-19
With that is now known
in the equation above
.
The concentration C of particles in the distance r from the center-point of the sun can with that calculated. Now is still missing in the start-equation A-1 the way W of the star-light. Because the summation of the deflection of the star-light during its way is not depending from the sequence of the summation, can take for the begin of the summation the point nearest to the sun too. The summation can make therefore in direction of W in fig. A2, what show off the sun. The connection between W and r is:
A-20
The start-equation A-1 is than:
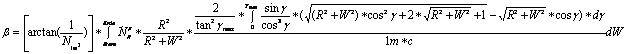A-21
Because these equation is not to integrate by me, was used follow approximations to the simplification:
To Chapter 2.5 Connection between the 3K-radiation and the deflection of light by the sun