A-22Simplifications
1. Simplification:
With neglecting of the crooking of the layer can used instead of the cosine-theorem for the estimation of L the simple cosine. With that follow in accordance with fig. A2:
A-22
But because for layers near R (big angles γ ) these simplification lead to very large L, is need a control of the simplification on these points (Fig. A5).
On ground of the first simplification
follow the formula for 
to:
A-23
A-24
A-25
And from
A-26
follow:
A-27
Because γ max is changed with W, remain C a complicated function of W.
The integral
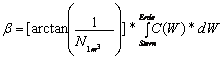
is now as before not to integrate by me.
Therefore is to take a second simplification:
2.Simplification:
Is used a calculation in sections
(Integration) for a length of way ∆W of the star-particle. Than is
assumed constant in the equation
in the area ∆W.
The dependence C from r respectively from W is but retain. Summation oft the deflection-angles for all ∆W give the complete deflection-angle.
Take the length of way ∆W as the distance from W1 to W2 . then follow
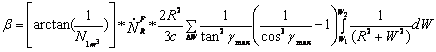A-28
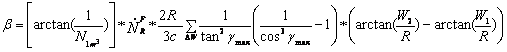A-29
The sum in these equation is calculated with EXCEL.
Now lead the division of the length of way ∆W up to the star to a lot of sections. Because is take a third simplification:
3. Simplification:
Enough distant from the sun is the
middle way-distance L in a 1m-layer near 1m. The concentration of sun-particles
in the layer is therefore nearly independent from the incidence-angle in the
layer and only depend from the distance r from the sun. The middle way-distance
on the point of begin of these simplification take
Begin and
that at the star take 1m. From these two numbers is used a average value.
The equation above
than simplifyed to
A-30
C is with that only a function of the variable W.
Far as to the third simplification.
All three simplifications are to control in the view to their effects.
Next is to consider the first simplification in view to the limit of its application:
As limit for application is taken: Lsimplify shall Lcos-theorem cross not more than 5%.
A-31
A-32
Because the deviation is greater for greater angles, is used γmax .
The results are to see in the follow table A1 in the column ABW (ABW=deviation).
|
Grad |
Bogen |
r |
Lmax-Satz |
Lmax-cos |
ABW in % |
W |
|
8,99999E+01 |
1,5708E+00 |
6,955000000E+08 |
3,610212E+04 |
5,730251E+05 |
1,487234E+03 |
1,213735E+03 |
|
8,9999E+01 |
1,5708E+00 |
6,955000001E+08 |
2,708313E+04 |
5,729645E+04 |
1,115577E+02 |
1,213863E+04 |
|
8,9998E+01 |
1,5708E+00 |
6,955000004E+08 |
2,022420E+04 |
2,864806E+04 |
4,165235E+01 |
2,427739E+04 |
|
8,9997E+01 |
1,5707E+00 |
6,955000010E+08 |
1,571000E+04 |
1,909867E+04 |
2,157010E+01 |
3,641615E+04 |
|
8,9996E+01 |
1,5707E+00 |
6,955000017E+08 |
1,267073E+04 |
1,432399E+04 |
1,304783E+01 |
4,855492E+04 |
|
8,9995E+01 |
1,5707E+00 |
6,955000026E+08 |
1,054341E+04 |
1,145918E+04 |
8,685754E+00 |
6,069368E+04 |
|
8,9994E+01 |
1,5707E+00 |
6,955000038E+08 |
8,993987E+03 |
9,549315E+03 |
6,174437E+00 |
7,283245E+04 |
|
8,9993E+01 |
1,5707E+00 |
6,955000052E+08 |
7,824838E+03 |
8,185125E+03 |
4,604405E+00 |
8,497121E+04 |
Tab.A1: Deviation of the length of way L of the particles by application of the simplification “cos” instead of “cos-theorem” (Lmax-Satz correspond Lmax-theorem)
From the table is obvious, that for angles more than 89,993° is to used the cos-theorem. (That is in according to column r about 5m from the calculate surface of the sun and in according to column W in a distance of about 85km, before the star-light reach its point nears the sun.)
The simplification, to use the cos instead of cos-theorem, has not only an effect to the length of way L, but to the radius b in fig. A4 too. The difference is make plain in fig. A5.
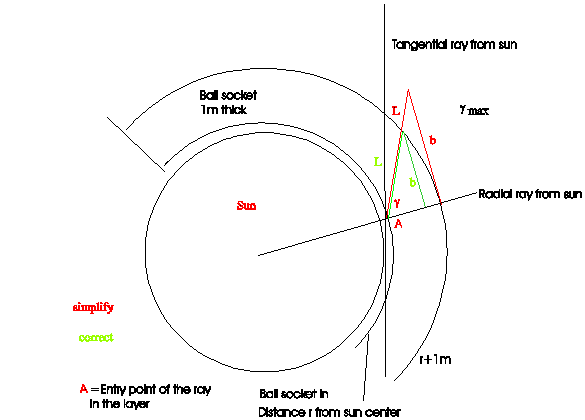
Fig. A5: Presentation of bsimple, bcorrect, Lsipmle and Lcorrect
Here is take the limit of application: bsimple shall bcorrect cross not more the 5%.
A-33
A-34
A-35
|
Grad |
Bogen |
r |
Lmax-Satz |
sin*Lmax |
b-einfach |
b-Abweich% |
|
8,99999E+01 |
1,5708E+00 |
6,955000000E+08 |
3,610212E+04 |
3,610212E+04 |
5,730251E+05 |
1,487234E+03 |
|
8,9999E+01 |
1,5708E+00 |
6,955000001E+08 |
2,708313E+04 |
2,708313E+04 |
5,729645E+04 |
1,115577E+02 |
|
8,9998E+01 |
1,5708E+00 |
6,955000004E+08 |
2,022420E+04 |
2,022420E+04 |
2,864806E+04 |
4,165235E+01 |
|
8,9997E+01 |
1,5707E+00 |
6,955000010E+08 |
1,571000E+04 |
1,571000E+04 |
1,909867E+04 |
2,157010E+01 |
|
8,9996E+01 |
1,5707E+00 |
6,955000017E+08 |
1,267073E+04 |
1,267073E+04 |
1,432399E+04 |
1,304783E+01 |
|
8,9995E+01 |
1,5707E+00 |
6,955000026E+08 |
1,054341E+04 |
1,054341E+04 |
1,145918E+04 |
8,685754E+00 |
|
8,9994E+01 |
1,5707E+00 |
6,955000038E+08 |
8,993987E+03 |
8,993987E+03 |
9,549315E+03 |
6,174437E+00 |
|
8,9993E+01 |
1,5707E+00 |
6,955000052E+08 |
7,824838E+03 |
7,824838E+03 |
8,185125E+03 |
4,604405E+00 |
Tab. A2: Deviation of b (Lmax-Satz correspond Lmax-theorem , b-einfach correspond bsimple and b-Abweich% correspond deviation of b in%)
From the table is to observe, that as for L also for angles more than 89,993° is to use the correct number of b.
The calculation of deflection-angle is therefore divided in two sections:
1. Calculation for angles γ<89,993°
2. Calculation for angles γ>89,993°
As far to control of the first simplification in view of its limit for application.
The second simplification with its in sections integration can only fill by a very fine division of the sections in W. The control can only follow by comparison with the target-number 1,75” of the deviation-angle.
The investigation of the third
simplification exist in the estimation of
Begin .
As is to see from column S (L-querF) of the table A4 in the line 109, is for an
angle of 2° the middle length of way 1,0002m, what is assess enough near to 1m.
This is take as limit of the third simplification.
To Chapter 2.5 Connection between the 3K-radiation and the deflection of light by the sun