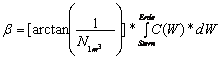Neue Seite 1

Calculation of the angles of deflection

The angles of deflection are calculated in follow steps (sections of distances):

1. From the nearest point of the star-light to the sun (W=0) up to angle γ_max =89,993° (W about 85 km)

2. From 89,993° up to 2°(W=1,9917*10¹⁰ m)

3. From 1,9917*10¹⁰ m up to 1AU (AU=Astronomic Unit= distance sun-earth=1,496*10¹¹m)

4. From 1AU up to star (W to infinite)

1. Section of distance:

The calculations from W≈0 (γ_max ≈90°) up to γ_max =89,993° (W about 85 km) are contained in the follow table A3.

Here are columns small make, to present the complete table. To can duplicate the calculations follow up the calculation-instructions of the columns.

The calculations in the table connect with follow formula:

The start-equation is as above to see

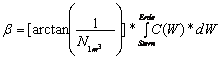A-1

Also above was given

C= A-7

and

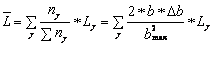A-9 with A-14

A-13

To here are not contain simplifications in the formulas. For integration but make now the second simplification for in sections integration with constant in the area of integration from W₁ to W₂. With that follow the start-equation

A-36

With these equation is calculable the deflection-angle for the way from W1 to W2 , where is take constant. That is the case in table A3 in each case for one group of 10 lines, for example from 12,139 km (89,9990°) up to 23,064 km (89,9981°) (yellow marked as limit). Follow 7 such groups. Summation over all groups for the angle-area from 89,9999°(W=1,2137 km) up to 89,9930° (W about 85 km) give the deflection-angle β₁ for the first above defined distance-section. That not begin at W=0 km, but about one km from the sun-nearest point of the star-light, can bear at the dimension of the sun.

A-37

Here is W_i the section of way for the group i (for example 12,139 km (89,9990°) up to 23,064 km (89,9981°)) and _Wi for the belonging to the middle length of way.

Because the factor before the sum is a constant, was calculated in table A3 only the sum . (It is 1,5130m; see the end of table.)

Now to the calculation of _Wi :

The equation above A-9 with A-14

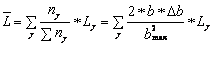
must divided for the area of angle from (0° up to 89,993°) and the over that going parts.

A-38

From

A-39

follow by transformation

A-40

and set in A-38:

A-41

For the next group of angles is the equation corresponding

A-42

The second term of sum in these equations is calculated in column M of the table (here SubdeltabL).

The complete equation is calculated in column N (here Lquer).

Grad

Bogen

Delta-W

Delta-Gamma

r (0,1m)

L Satz

delta b

Konstante

bdeltabL

SubdeltabL

Lquer

Lquerarctan

8,99999E+01

1,2137E+03

3,6102E+04

Lquer89993

8,99998E+01

2,4276E+03

3,4947E+04

###

8,99997E+01

3,6415E+03

3,3832E+04

8,99996E+01

4,8554E+03

3,2755E+04

8,99995E+01

6,0692E+03

3,1717E+04

###

2,4779E+04

3,8922E-01

8,99994E+01

7,2831E+03

3,0717E+04

8,99993E+01

8,4970E+03

2,9755E+04

8,99992E+01

9,7109E+03

2,8829E+04

8,99991E+01

1,0925E+04

2,7938E+04

8,99990E+01

1,2139E+04

2,7083E+04

8,99989E+01

1,3352E+04

2,6262E+04

8,99988E+01

1,4566E+04

2,5473E+04

8,99987E+01

1,5780E+04

2,4717E+04

8,99986E+01

1,6994E+04

2,3991E+04

8,99985E+01

1,8208E+04

2,3295E+04

###

1,8522E+04

3,2326E-01

8,99984E+01

1,9422E+04

2,2628E+04

8,99983E+01

2,0636E+04

2,1989E+04

8,99982E+01

2,1850E+04

2,1375E+04

8,99981E+01

2,3064E+04

2,0788E+04

8,99980E+01

2,4277E+04

2,0224E+04

8,99979E+01

2,5491E+04

1,9684E+04

8,99978E+01

2,6705E+04

1,9166E+04

8,99977E+01

2,7919E+04

1,8669E+04

8,99976E+01

2,9133E+04

1,8193E+04

8,99975E+01

3,0347E+04

1,7736E+04

###

1,3759E+04

2,4013E-01

8,99974E+01

3,1561E+04

1,7297E+04

8,99973E+01

3,2775E+04

1,6876E+04

8,99972E+01

3,3988E+04

1,6472E+04

8,99971E+01

3,5202E+04

1,6083E+04

8,99970E+01

3,6416E+04

1,5710E+04

8,99969E+01

3,7630E+04

1,5351E+04

8,99968E+01

3,8844E+04

1,5006E+04

8,99967E+01

4,0058E+04

1,4675E+04

8,99966E+01

4,1272E+04

1,4355E+04

8,99965E+01

4,2486E+04

1,4048E+04

###

1,0626E+04

1,8546E-01

8,99964E+01

4,3699E+04

1,3752E+04

8,99963E+01

4,4913E+04

1,3467E+04

8,99962E+01

4,6127E+04

1,3192E+04

8,99961E+01

4,7341E+04

1,2926E+04

8,99960E+01

4,8555E+04

1,2671E+04

8,99959E+01

4,9769E+04

1,2424E+04

8,99958E+01

5,0983E+04

1,2186E+04

8,99957E+01

5,2197E+04

1,1955E+04

8,99956E+01

5,3410E+04

1,1733E+04

8,99955E+01

5,4624E+04

1,1518E+04

###

8,5148E+03

1,4861E-01

8,99954E+01

5,5838E+04

1,1310E+04

8,99953E+01

5,7052E+04

1,1109E+04

8,99952E+01

5,8266E+04

1,0914E+04

8,99951E+01

5,9480E+04

1,0726E+04

8,99950E+01

6,0694E+04

1,0543E+04

8,99949E+01

6,1908E+04

1,0367E+04

8,99948E+01

6,3121E+04

1,0195E+04

8,99947E+01

6,4335E+04

1,0029E+04

8,99946E+01

6,5549E+04

9,8676E+03

8,99945E+01

6,6763E+04

9,7112E+03

###

7,0304E+03

1,2270E-01

8,99944E+01

6,7977E+04

9,5593E+03

8,99943E+01

6,9191E+04

9,4118E+03

8,99942E+01

7,0405E+04

9,2685E+03

8,99941E+01

7,1619E+04

9,1293E+03

8,99940E+01

7,2832E+04

8,9940E+03

8,99939E+01

7,4046E+04

8,8624E+03

8,99938E+01

7,5260E+04

8,7344E+03

8,99937E+01

7,6474E+04

8,6099E+03

###

5,9392E+03

1,0366E-01

8,99936E+01

7,7688E+04

8,4887E+03

8,99935E+01

7,8902E+04

8,3707E+03

8,99934E+01

8,0116E+04

8,2558E+03

8,99933E+01

8,1330E+04

8,1439E+03

8,99932E+01

8,2543E+04

8,0348E+03

8,99931E+01

8,3757E+04

7,9285E+03

8,99930E+01

8,4971E+04

7,8248E+03

1,5130E+00

Tab. A3: The calculation from W=1214m up to W=84971m ( The yellow marked cells make plain the limits of groups.)

Instructions for calculations oft he columns in the table above:

A: Entry-angle of the sun-rays in the 1m-layer (angle measured from radial-ray), begin at 89,9930°, sequence of stages in (1/10 000)°-steps; end at 89,9999°. The angle A can act as γ_max too.

B: Conversion to arc: B=(A/180)*π

C: Length of way W, calculated from radius of the sun and γ_max :

C=695500000/TAN(3,141592654*A/180) The angle A is here used as γ_max (see fig. A2 too).

D: Difference of the length of way W between two numbers of angles, is at these table but not used.

E: A fifth of the difference of angle, is at these table but not used.

F: Radius of the sun as a constant: F=6,955*10⁸

G: Distance r of the layer from center-point of the sun: G= WURZEL(C²+F²)

H: length of course L of the particles in the layer by the equation above . Here is to take for r the number belonging to γ_max , see fig. A3 too. An example: For the range of angles from 89,9981° up to 89,9990° shall calculated . To that is divided the range of angles in 10 sections (Line 11 to 20): from 89,9981° over 89,9982° to just 89,9990° (γ_max). For each angle is calculated L_γ by the equation above, where is used for r the number belonging to 89,9990°.

H=WURZEL(($G$11)²*cos²(B)+2*$G$11+1)-$G$11*cos(B)

(Note: WURZEL correspond to square rote)

I: Calculation of b in accordance to fig. A5: I=sin(B)*H

J: Calculation of the difference ∆b in accordance to fig. A4: J=I_i-I_i+1

K: A constant: The middle course for the range from 0° up to 89,993° as part of the sum 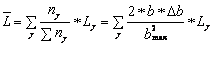. It is take from tab. A4, column S (Lquer), line 1. K=5103,6

L: The product b*∆b*L: Column L=I*J*H

M: The sum b*∆b*L: M=2/(I11)²*SUMME(L11:L20) for example for the section line 11 to 20.

N: The middle length of course in accordance to

N=N(of the group of angles before)*(b_{max group before}/b_max )²+M

O: Calculation of each term of sum of the equation:

O=N*(arctan(W₂/R)-arctan(W₁/R)) with W₁and W₂ for the respective group of angles

The sum of the numbers of the column O is the searched value of the term

for the first area of distance W=1,2137 km up to W≈85 km.

The result of table A3 is: 1,5130m.

To Chapter 2.5 Connection between the 3K-radiation and the deflection of light by the sun

List of contents

Back to the start