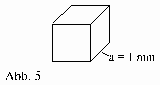
4.3 Quantitative Bestimmung der Struktur
4.3.1 Bestimmung des mittleren Abstandes zwischen zwei Teilchen
Bei der quantitativen Bestimmung wird zunächst der Zustand im freien Raum entsprechend der Darstellung in Abb.1 betrachtet. Grundlegend dabei ist der mittlere Abstand von zwei benachbarten Teilchen, weil das für die Verbindung zu l und damit zu den bekannten Größen der elektromagnetischen Wellen erforderlich ist. Der freie Raum ist von elektromagnetischen Wellen durchsetzt, ein Hohlraum auch. Ein Hohlraum kann als schwarzer Körper angesehen werden. In ihm stellt sich nur abhängig von der Temperatur ein bestimmtes Spektrum der Strahlung ein. Eine eben solche Strahlung trifft als 3 K-Strahlung aus allen Richtungen des Weltraumes auf die Erde. Es ist daher eine besondere Strahlung, die keiner Richtung den Vorzug gibt und somit von grundlegender Natur ist. Es liegt nahe, aus dieser Strahlung den gesuchten mittleren Abstand zu gewinnen:
Bekannt ist lt. /1/: bei 3 K: 103 Photonen / cm3, das sind 1 Photon / mm3
Daraus folgt für den Raum eines Photons ein Würfel mit der Kantenlänge von a= 1mm (Abb.5):
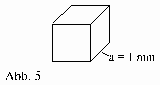
Das ist zwar der Raum eines Photons oder nach obiger Beschreibung für ein l, sagt aber noch nichts über den Abstand zweier benachbarter Teilchen aus.
Denkt man sich alle in einem bestimmten Volumen vorhandenen l nach der Größe geordnet und vereinfacht durch einen Pfeil dargestellt, so entspricht das etwa folgendem Bild (Abb.6):
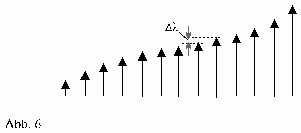
Da es eine endliche Anzahl von l sind, ist eine solche Anordnung möglich. In einem bestimmten Bereich gibt es besonders viele nahezu gleich große l. Das ist der Bereich um lmax in der Verteilungskurve der elektromagnetischen Strahlung. Der Bereich kleinerer und größerer l kann möglicherweise als statistische Abweichung betrachtet werden.
Stellt man nun die Frage, um welche Länge Dl sich ein l im Bereich lmax vergrößert, wenn man von einem l zum nächst größeren l übergeht, so erhält man als Antwort auch den gesuchten mittleren Abstand von zwei Teilchen (Abb.7).
Dargestellt:
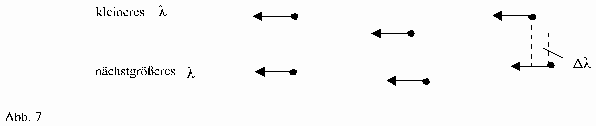
Die Problematik des Abstandes zweier benachbarter Teilchen war bei der Suche nach dem Mechanismus für die Rotverschiebung aufgetaucht.
Es war die Wegstrecke der Lichtteilchen zwischen zwei 3er-Stößen gefragt. Dazu wiederum ist der Abstand von zwei Teilchen im 3 K-Welt-Raum von Bedeutung.
Bekannt ist die volumenbezogene Anzahl von Photonen im Frequenzbereich dn, geltend für eine bestimmte Temperatur und die
Strahlung eines schwarzen Körpers:
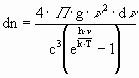
Weil hier Abstände von Interesse sind, wird von n auf l übergegangen mit:
![]()
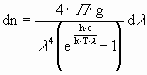
Um den Abstand zweier benachbarter Teilchen des 3 K-Welt-Raumes zu erhalten, bietet sich hier die Frage an:
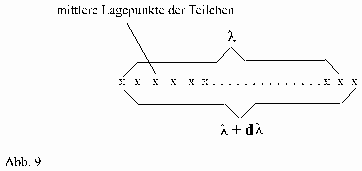
"Wie groß müsste dl sein, damit dn um ein Photon steigt und somit das nächstliegende Teilchen gefunden wird?" Zur Verdeutlichung siehe Abb.8 und Abb.9:
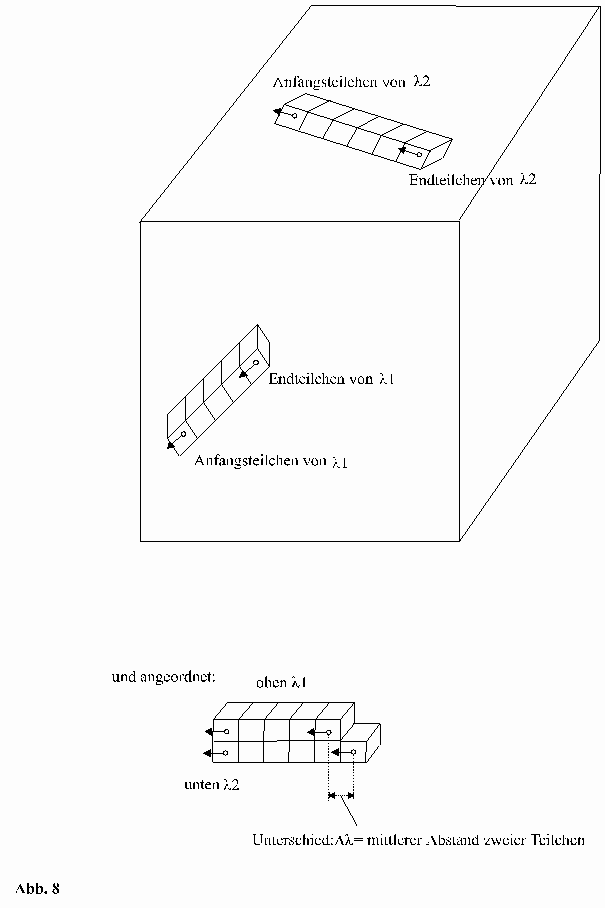
vereinfacht dargestellt:
Mit D n = 1 und
![]()
wird
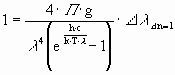
Der Wert von g ist für eine in 2 Komponenten zerlegbare elektromagnetische
Welle
mit 2 anzusetzen.
Zur quantitativen Auswertung sind T und l festzulegen:
Für T wird der Wert aus den Messungen des Satelliten COBE verwendet:
T = (2,726 ± 0,004)o K.
Für l stehen alle Wellenlängen zur Auswahl.
Es ist sicher zweckmäßig, die am häufigsten vorkommende Wellenlänge zu verwenden und die anderen als statistische Abweichungen zu betrachten.
Auch aus den COBE-Messungen ist lmax=1,05mm bekannt.
Damit wird der gesuchte mittlere Abstand zwischen zwei benachbarten Teilchen:
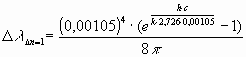
![]()
Dieser Wert wird bei der Behandlung der Beispielrechnungen eine fundamentale Rolle spielen.
Bei der Problematik der Lichtablenkung in Sonnennähe erwies sich eine andere gedachte Anordnung der Teilchen aus einem bestimmten Volumen, z.B. 1m3, als zweckmäßig:
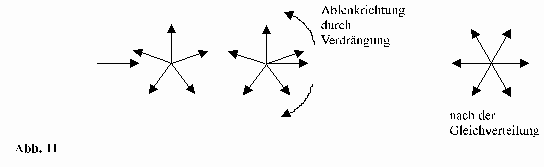
Alle Teilchen werden in einen Ursprungspunkt gelegt und unterscheiden sich nur durch die Richtung, dargestellt als Pfeil, in der sie aus dem Punkt austreten (Abb.10):
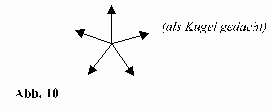
Damit ist die Anzahl von Richtungen festgelegt, die es in diesem Volumen gleichzeitig gibt.
Die Richtungen sind im wenig durch Strukturen wie Licht oder Masseteilchen gestörten Raum wohl gleich verteilt. Gelangt ein Photon in diesen Raum, ist es in das Strahlenbündel aus dem Mittelpunkt einzubeziehen.
Der angestrebte Ausgleich zur Gleichverteilung drängt über Zusammenstöße alle anderen Teilchen etwas aus ihrer bisherigen Richtung heraus (Abb.11):