5.2.3 Umsetzung in Formeln
Setzt man den Wert des Richtungsvektors des Sonnenlicht-Teilchens mit 1 an,
so erhalten die z.B. in dem betrachteten Raumvolumen von 1m3
vorhandenen N1m3 Teilchen jeweils
einen Richtungsänderungsvektor mit dem Wert
![]()
(verursacht durch nur dieses eine Sonnenlicht-Teilchen)
Die Richtung ändert sich für alle Teilchen in dem 1m3 zur Sonne hin (siehe Abb. 15d).
N1m3 ist dabei zu bestimmen als:
N1m3 =
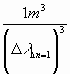
Dieser Richtungsänderungsvektor verursacht den Änderungswinkel
![]() .
.
Darstellung für ein Sonnenlicht-Teilchen (Abb.16):
(mit der Abkürzung S-Teilchen für Sonnenlicht-Teilchen)
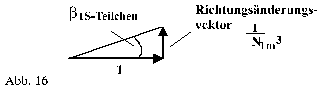
Daraus lässt sich der Ablenkwinkel
![]() berechnen, den
ein 3 K-Teilchen und damit auch das Sternlicht-Teilchen bei dem Eindringen von
einem Sonnenlicht-Teilchen in den betrachteten 1m3 erfährt:
berechnen, den
ein 3 K-Teilchen und damit auch das Sternlicht-Teilchen bei dem Eindringen von
einem Sonnenlicht-Teilchen in den betrachteten 1m3 erfährt:
![]()
![]() =
=
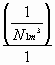 ;
;
![]() =
arctan
=
arctan![]()
Nun zur Wegstrecke des Sternlicht-Teilchens, auf dem diese Ablenkung erfolgt:
Der betrachtete 1m3 sei ein Würfel und so gelegt, dass das
Sternlicht senkrecht auf eine Fläche trifft. Der zurückgelegte Weg der
Sternlicht-Teilchen, auf dem die Ablenkung
![]() erfolgt ist
damit die Kantenlänge des Würfels von 1m3.
erfolgt ist
damit die Kantenlänge des Würfels von 1m3.
Die Ablenkung des Sternlichtes während des Durchlaufens einer Strecke von 1m und verursacht durch nur ein Sonnenlicht-Teilchen ist:
![]() =
= ![]()
![]()
Das bezog sich jetzt auf ein Sonnenlicht-Teilchen.
Durch die Anzahl NS Sonnenlicht-Teilchen in dem 1m3 wird die Ablenkung entsprechend vielfach:

Bestimmung von NS:
Nun sind je nach Entfernung von der Sonne unterschiedlich viele Sonnenlicht-Teilchen in einem m3 enthalten. Auf dem Weg des Sternlichtes steigt ihre Konzentration bis zur Sonne an. Entfernt sich das Sternlicht wieder von der Sonne, nimmt die Konzentration der Sonnenlicht-Teilchen ab. Die Anzahl der von der Sonne gekommenen Teilchen NS je m3 im Abstand r von der Sonne kann wie folgt beschrieben werden:
mit dS = Sonnendurchmesser und
![]() = Anzahl von
Sonnenlicht-Teilchen an der Sonnenoberfläche bei
= Anzahl von
Sonnenlicht-Teilchen an der Sonnenoberfläche bei
![]() im
Volumen von 1m3.
im
Volumen von 1m3.
Die Teilchenkonzentration nimmt entsprechend der größeren Kugelfläche beim Abstand r ab:
![]()
![]()
![]()
Der Zusammenhang des Abstandes r mit dem Wegstück (![]() )
der Sternlicht-Teilchen ergibt sich aus folgendem Bild (Abb.17):
)
der Sternlicht-Teilchen ergibt sich aus folgendem Bild (Abb.17):

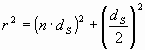
Damit wird die Anzahl NS Sonnenlicht-Teilchen in der Entfernung
![]() von der Sonne in einem m3:
von der Sonne in einem m3:
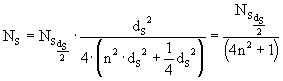
und die Ablenkung in Grad je m Lauflänge des Sternlichtes:
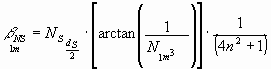
Nun zur gesamten Lauflänge des Sternlichtes (siehe Abb.17):
Für eine vom Sternlicht-Teilchen durchlaufene Strecke
![]() wird dafür die
wird dafür die
Ablenkung
![]() :
:
![]()
![]()
![]()
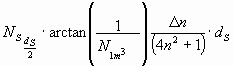
Summation über alle Dn vom Stern (weit entfernt: ¥ ) bis zur Sonne und Übergang von Dn auf dn liefert:
![]()
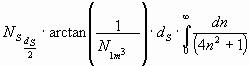
Die Integration ergibt ![]() und mit dem Faktor annähernd
2 für den Weg auch von der Sonne weg bis zur Erde wird der gesuchte Ablenkwinkel
a des Sternlichtes durch die
Sonne:
und mit dem Faktor annähernd
2 für den Weg auch von der Sonne weg bis zur Erde wird der gesuchte Ablenkwinkel
a des Sternlichtes durch die
Sonne:
![]()
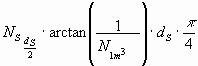

(Der Faktor annähernd 2 kann verwendet werden, da sich die Hauptwechselwirkungen nahe der Sonne abspielen.)